
量子力学周世勋(全套通用).ppt

YY****。。







亲,该文档总共544页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

量子力学周世勋(全套通用).ppt
量子力学使用标准条件3。连续:能量最低的态称为基态,其上为第一激发态、第二激发态依次类推。第四章量子力学中的力学量利用波函数标准条件:当|x|→∞时ψ,→0。其正交归一条件为:(3)角动量算符的对易关系例:证明在LZ本征态Ylm下,<Lx>=<Ly>=0由角动量对易关系:§3电子在库仑场中的运动(二)求解Schrodinger方程(三)使用标准条件定解最高幂次项的νmax=nr将β=n代入递推公式:总波函数为:使用球函数的归一化条件:下面列出了前几个径向波函数Rnl表达式:(1)本征值和本征函数(3)简

量子力学+周世勋(全套课件).ppt
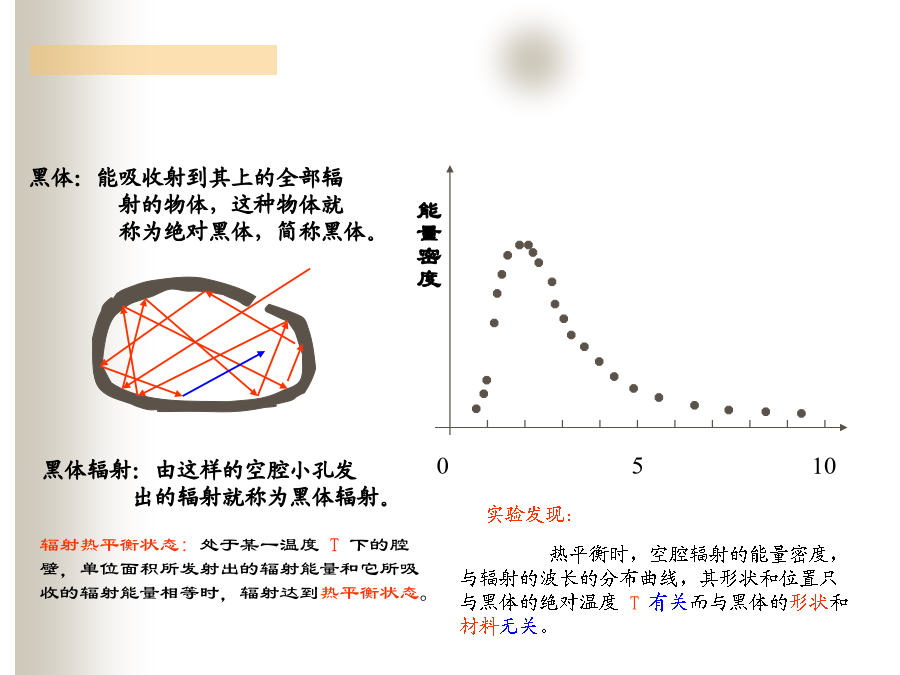
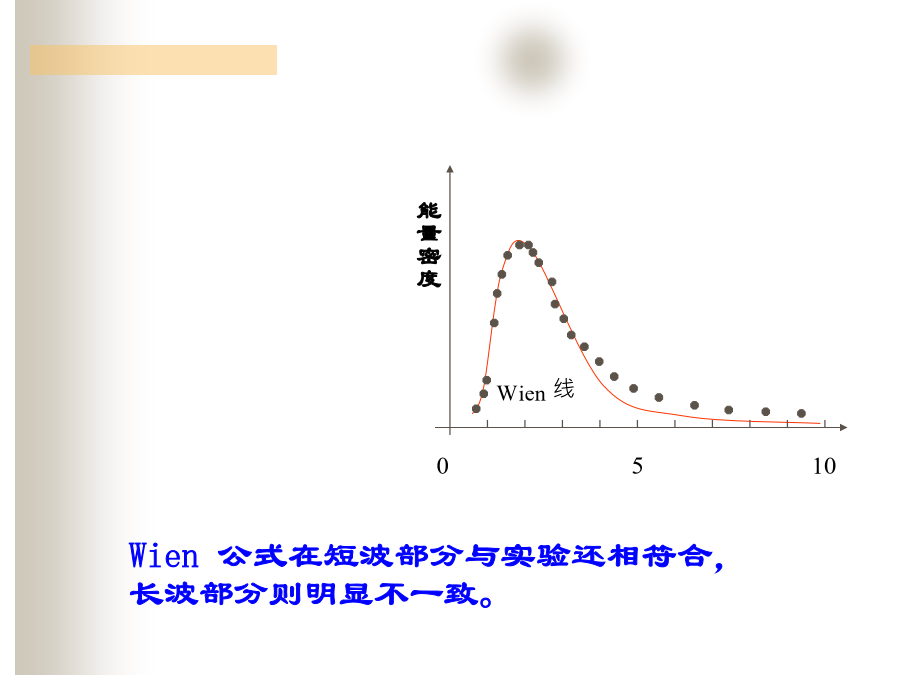
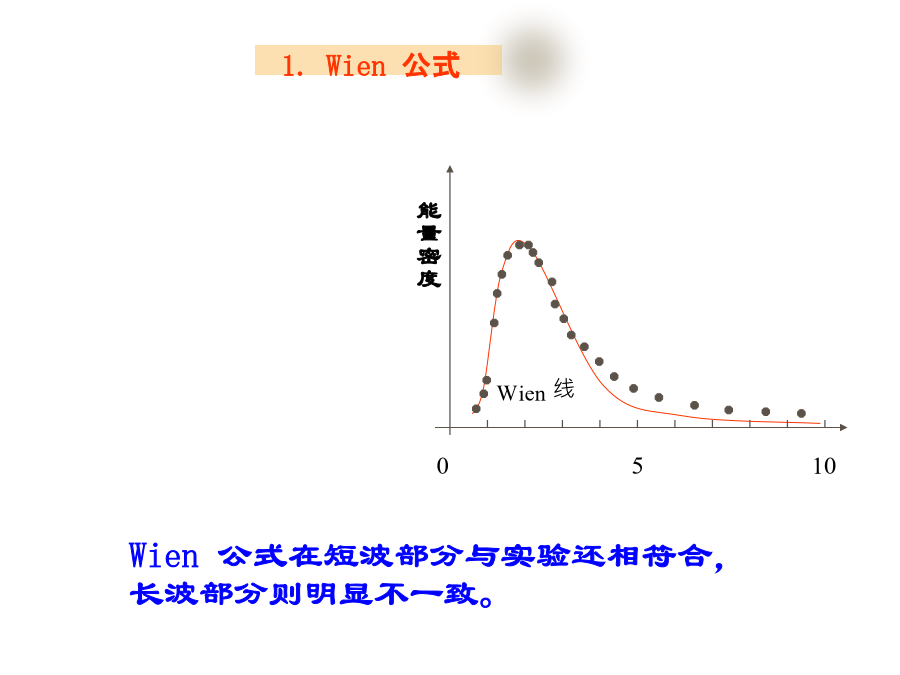
量子力学目录第一章量子力学的诞生§1经典物理学的困难(二)经典物理学的困难黑体:能吸收射到其上的全部辐射的物体,这种物体就称为绝对黑体,简称黑体。Wien线1.Wien公式1.Wien公式(2)光电效应(3)原子光谱,原子结构人们自然会提出如下三个问题:从前,希腊人有一种思想认为:自然之美要由整数来表示。例如:奏出动听音乐的弦的长度应具有波长的整数倍。§2量子论的诞生§2量子论的诞生(一)Planck黑体辐射定律该式称为Planck辐射定律对Planck辐射定律的三点讨论:对Planck辐射定律的三点讨论

量子力学周世勋全套学习教案.ppt
会计学空白(kòngbái)演示感谢您的观看(guānkàn)!内容(nèiróng)总结

(完整版)量子力学+周世勋(全套课件).ppt
量子力学目录第一章量子力学的诞生§1经典物理学的困难(二)经典物理学的困难黑体:能吸收射到其上的全部辐射的物体,这种物体就称为绝对黑体,简称黑体。Wien线1.Wien公式1.Wien公式(2)光电效应(3)原子光谱,原子结构人们自然会提出如下三个问题:从前,希腊人有一种思想认为:自然之美要由整数来表示。例如:奏出动听音乐的弦的长度应具有波长的整数倍。§2量子论的诞生§2量子论的诞生(一)Planck黑体辐射定律该式称为Planck辐射定律对Planck辐射定律的三点讨论:对Planck辐射定律的三点讨论

量子力学周世勋课后答案.docx
量子力学课后习题详解第一章量子理论基础1.1由黑体辐射公式导出维恩位移定律:能量密度极大值所对应的波长与温度T成反比,即T=b(常量);并近似计算b的数值,准确到二位有效数字。解根据普朗克的黑体辐射公式,(1)以及,(2),(3)有这里的的物理意义是黑体内波长介于λ与λ+dλ之间的辐射能量密度。本题关注的是λ取何值时,取得极大值,因此,就得要求对λ的一阶导数为零,由此可求得相应的λ的值,记作。但要注意的是,还需要验证对λ的二阶导数在处的取值是否小于零,如果小于零,那么前面求得的就是要求的,具体如下:如果令
