
蒙特卡洛方法概述.ppt

YY****。。








亲,该文档总共63页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

蒙特卡洛方法概述.ppt
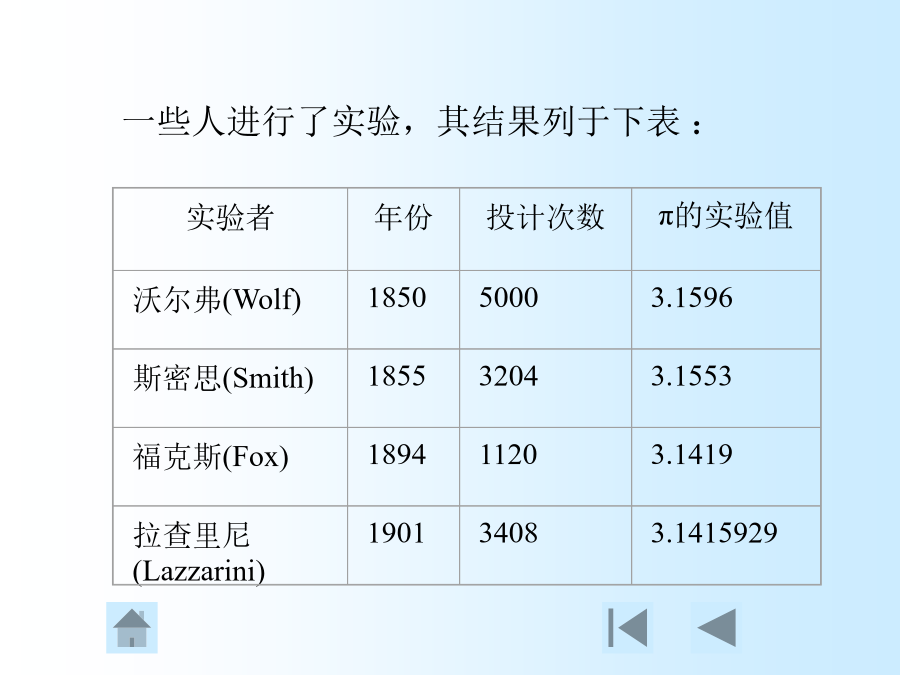
第一章蒙特卡罗方法概述第一章蒙特卡罗方法概述蒙特卡罗方法的基本思想例1.蒲丰氏问题一些人进行了实验,其结果列于下表:例2.射击问题(打靶游戏)现假设该运动员进行了N次射击,每次射击的弹着点依次为r1,r2,…,rN,则N次得分g(r1),g(r2),…,g(rN)的算术平均值代表了该运动员的成绩。换言之,为积分<g>的估计值,或近似值。在该例中,用N次试验所得成绩的算术平均值作为数学期望<g>的估计值(积分近似值)。基本思想因此,可以通俗地说,蒙特卡罗方法是用随机试验的方法计算积分,即将所要计算的积分看作

蒙特卡洛方法概述.ppt
第一章蒙特卡罗方法概述第一章蒙特卡罗方法概述蒙特卡罗方法的基本思想例1.蒲丰氏问题一些人进行了实验,其结果列于下表:例2.射击问题(打靶游戏)现假设该运动员进行了N次射击,每次射击的弹着点依次为r1,r2,…,rN,则N次得分g(r1),g(r2),…,g(rN)的算术平均值代表了该运动员的成绩。换言之,为积分<g>的估计值,或近似值。在该例中,用N次试验所得成绩的算术平均值作为数学期望<g>的估计值(积分近似值)。基本思想因此,可以通俗地说,蒙特卡罗方法是用随机试验的方法计算积分,即将所要计算的积分看作

蒙特卡洛方法概述.ppt
第一章蒙特卡罗方法概述第一章蒙特卡罗方法概述蒙特卡罗方法的基本思想例1.蒲丰氏问题一些人进行了实验,其结果列于下表:例2.射击问题(打靶游戏)现假设该运动员进行了N次射击,每次射击的弹着点依次为r1,r2,…,rN,则N次得分g(r1),g(r2),…,g(rN)的算术平均值代表了该运动员的成绩。换言之,为积分<g>的估计值,或近似值。在该例中,用N次试验所得成绩的算术平均值作为数学期望<g>的估计值(积分近似值)。基本思想因此,可以通俗地说,蒙特卡罗方法是用随机试验的方法计算积分,即将所要计算的积分看作

蒙特卡洛方法.pdf

蒙特卡洛方法MC方法.doc
蒙特卡洛方法MC方法蒙特卡洛方法MC方法蒙特卡洛方法MC方法MCC方法蒙特卡罗方法的诞生蒙特卡罗方法的产生可追溯到Buffon投针实验。法国数学家Buffon用此实验来估算p值,它的原理是这样子的:在桌面上划一组间距为d的平行线,然后向桌面上随意抛掷长度为L的细针,从针与平行线相交的概率就可以得到p值.其中由积分性质可得投针置于平行线上的概率为假如在N次投针实验中,有M次与平行线相交,则有dL图3.2Buffon的投针实验dAxLsinx图3。3投针位置分析1930年,费米利用蒙特卡罗方法研究了中子的扩散
