系统建模与系统分析.ppt

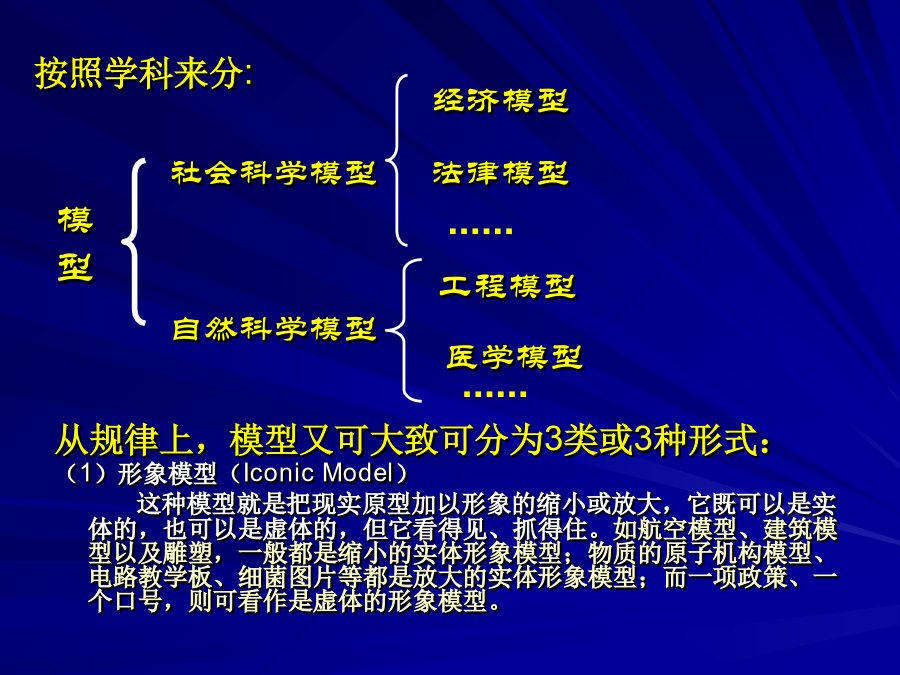
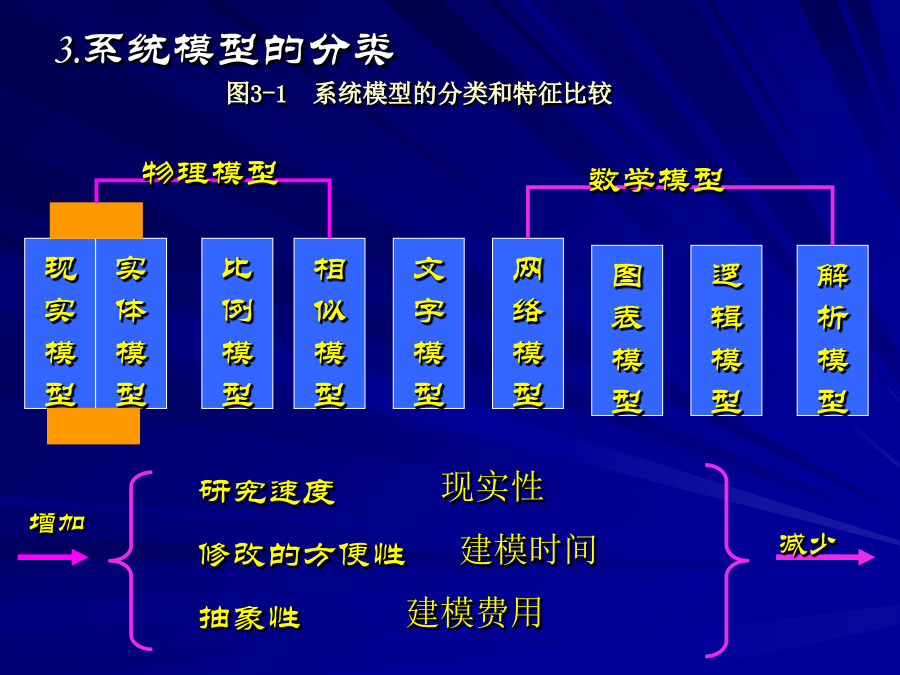
第三章系统模型与系统分析重点问题3.1系统模型模型的含义很广泛：
自然科学和工程技术中：概念、公式、定律、理论等。
社会科学中：学说、原理、政策、小说、美术、语言
Newton第二定律是物体在力的作用下，其运动规律这个原型的一种模型；
计算机是人的某些功能或智能这个原型的一种模型；
一张照片是某种实体（如人）的反映；
一场戏剧是某类事件的再现；
吃饭这句话是人往嘴里面送东西，达到充饥的动作的抽象……2.为什么要使用系统模型
人类认识和改造客观世界的两种研究方法——实验法和模型法。
系统开发的需要（预测、分析、优化和评价）
经济上的考虑
安全性、稳定性上的考虑
时间上的考虑
系统模型容易操作，分析结果易于理解3.系统模型的分类按照学科来分:（2）模拟模型（AnalogModel）3.系统模型的分类二、系统建模方法2.建模的主要方法

(1)推理法（“白箱”问题）
(2)实验法（“黑箱”或“灰箱”问题）
(3)统计分析法（“黑箱”问题）
(4)混合法
(5)类似法（相似模型）系统结构模型化技术理解系统结构的概念

（构成系统诸要素间的关联方式或关系）及其有向图（节点与有向弧）和矩阵（可达矩阵等）这两种常用的表达方式。

比较有代表性的系统结构分析方法有：

关联树（如问题树、目标树、决策树）法、解释结构模型化（ISM）方法、系统动力学（SD）结构模型化方法等。ISM解释结构模型ISM实用方法基础(2)有向图表示

图论基本知识：
图、邻接、关联、有向图
有向图表示：
节点、有向边、
通路、路长、
回路
环（3）矩阵表达三、ISM实用化方法步骤及应用第5步：提取骨架矩阵，分为三步：
（1）去强连接要素得缩减矩阵；（2）去越级二元关系；
（3）去单位阵得骨架矩阵；
第6步：作出多级递阶有向图。作图过程为：
（1）分区域逐级排列系统要素；
（2）将缩减掉的要素随其代表要素同级补入，并标明其间的相互作用关系；
（3）用从下到上的有向弧来显示逐级要素间的关系；
（4）补充必要的越级关系。
第7步：经直接转换，建立解释结构模型。影响部门执行力因素分析要素关系分析图（图1）通过上述分析，我们认为一个组织执行力的提高，从长期性和根本上来说，取决于这个组织的战略定位（1）、制度与规范的建设能力（9）和领导者的素质、修养及能力（5），从短期性和直接性来说，与工作计划（4）、有效控制（8）和组织成员间的相互配合与协调能力（10）等要素直接相关，而组织文化与成员素质（责任心）则直接影响以上三个要素。所以我们提出了根据组织战略定位，加强组织文化建设，提高组织成员素质（责任心），优化工作流程，加强工作制度建设，全面提高本部门执行力的初步方案（措施）。ISM的工作程序ISM的优点及不足主成分分析主成分分析
主成分回归
立体数据表的主成分分析一项十分著名的工作是美国的统计学家斯通(stone)在1947年关于国民经济的研究。他曾利用美国1929一1938年各年的数据，得到了17个反映国民收入与支出的变量要素，例如雇主补贴、消费资料和生产资料、纯公共支出、净增库存、股息、利息外贸平衡等等。在进行主成分分析后，竟以97.4％的精度，用三新变量就取代了原17个变量。根据经济学知识，斯通给这三个新变量分别命名为总收入F1、总收入变化率F2和经济发展或衰退的趋势F3。更有意思的是，这三个变量其实都是可以直接测量的。斯通将他得到的主成分与实际测量的总收入I、总收入变化率I以及时间t因素做相关分析，得到下表：
主成分分析是把各变量之间互相关联的复杂关系进行简化分析的方法。
在社会经济的研究中，为了全面系统的分析和研究问题，必须考虑许多经济指标，这些指标能从不同的侧面反映我们所研究的对象的特征，但在某种程度上存在信息的重叠，具有一定的相关性。
主成分分析试图在力保数据信息丢失最少的原则下，对这种多变量的截面数据表进行最佳综合简化，也就是说，对高维变量空间进行降维处理。
很显然，识辨系统在一个低维空间要比在一个高维空间容易得多。

(1)基于相关系数矩阵还是基于协方差矩阵做主成分分析。当分析中所选择的经济变量具有不同的量纲，变量水平差异很大，应该选择基于相关系数矩阵的主成分分析。
（2）选择几个主成分。主成分分析的目的是简化变量，一般情况下主成分的个数应该小于原始变量的个数。关于保留几个主成分，应该权衡主成分个数和保留的信息。
（3）如何解释主成分所包含的经济意义。
二、主成分分析的数学模型与几何解释这种由讨论多个指标降为少数几个综合指标的过程在数学上就叫做降维。主成分分析通常的做法是，寻求原指标的线性组合Fi。满足如下的条件：••••为了方便，我们在二维空间中讨论主成分的几何意义。设有n个样品，每个样品有两个观测变量xl和x2，在由变量xl和x2所确定的二维平面中，n个样本点