基于分数傅立叶变换的形状描述方法.pdf

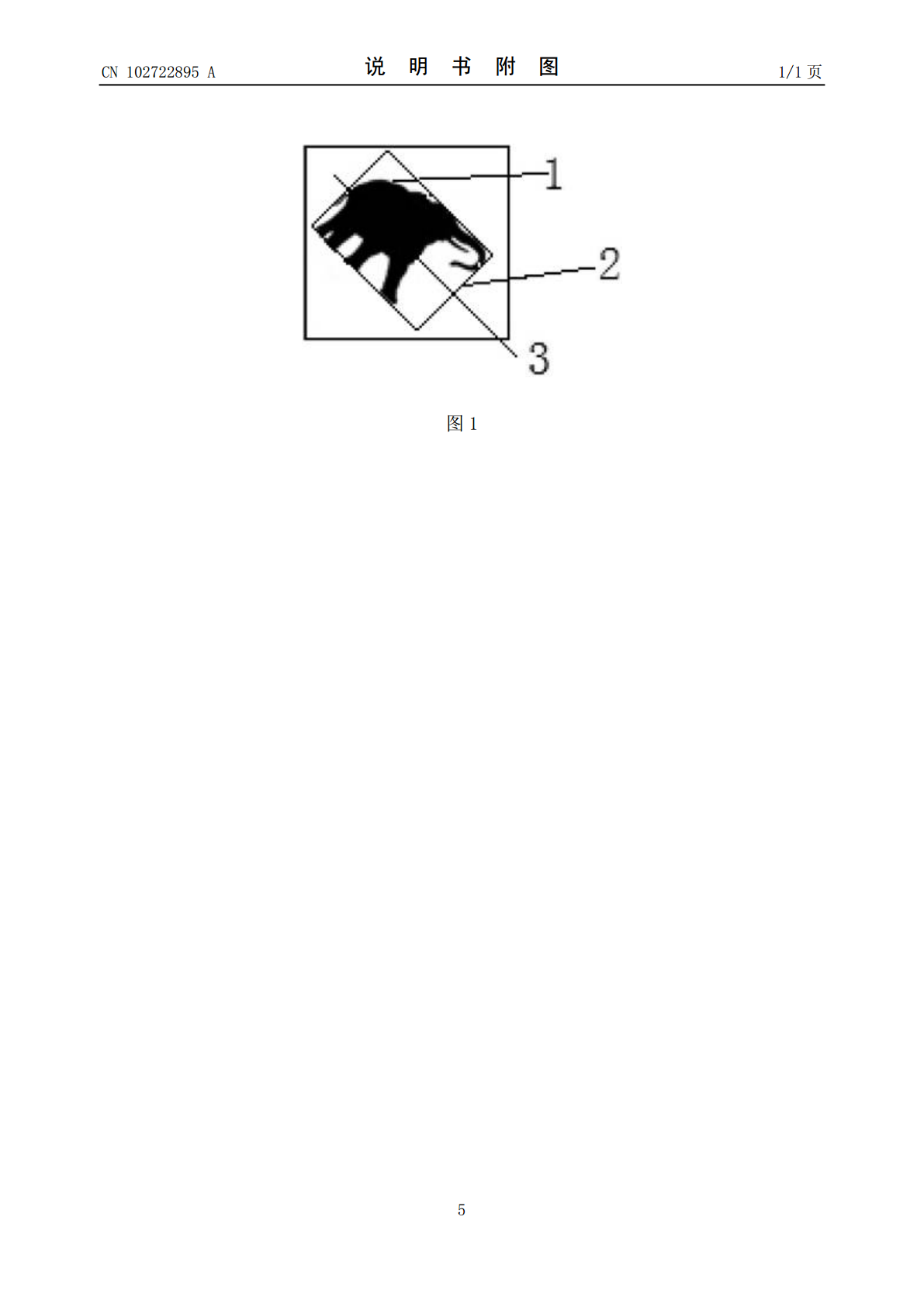
(19)中华人民共和国国家知识产权局*CN102722895A*(12)发明专利申请(10)申请公布号CN102722895A(43)申请公布日2012.10.10(21)申请号201210150026.5(22)申请日2012.05.15(71)申请人哈尔滨工程大学地址150001黑龙江省哈尔滨市南岗区南通大街145号哈尔滨工程大学科技处知识产权办公室(72)发明人郑丽颖石大明(51)Int.Cl.G06T9/20(2006.01)权利要求书权利要求书1页1页说明书说明书22页页附图附图11页(54)发明名称基于分数傅立叶变换的形状描述方法(57)摘要本发明提供的是一种基于分数傅立叶变换的形状描述方法。其步骤是：第一步，估计图像中目标物体的质心和主轴方向；第二步，将图像旋转和平移；第三步，去除旋转和平移之后的图像中的目标外接矩形之外的部分，得到目标图像，并将目标图像的大小进行归一化；第四步，计算归一化图像的不同阶数的分数傅立叶变换；第五步，舍弃分数傅里叶变换的幅值，仅保留相位；第六步，将归一化图像的各阶分数傅立叶变换的相位直方图作为物体的形状特征。本发明所提出的形状描述方法具有旋转和平移不变性以及利用分数傅里叶变换相位的特点，实现了图像在不同尺度上的滤波，保证了使得所描述的特征既和物体的边界轮廓有关，又与物体的内部区域有关。CN1027895ACN102722895A权利要求书1/1页1.一种基于分数傅立叶变换的形状描述方法，其特征在于包括以下步骤：设I为的输入图像矩阵，I中只包含一个目标，且目标为黑色，背景为白色，第一步，估计图像中物体的质心和主轴方向，具体为：根据（1）计算目标的质心：TOc＝[M10/M00,M01/M00](1)其中，变量k和l的取值为0或者1，Mkl表示图像的(k+l)阶矩，Oc为图像中目标的质心，W和H分别为图像的宽度和高度；I(h,w)表示输入图像矩阵I的第h行第w列的元素；根据目标的最小外接矩形估计物体主轴方向；第二步，根据主轴方向和质心建立新的坐标系，其中坐标原点为质心，主轴方向为x轴，按照新的坐标系将输入图像矩阵I平移和旋转，得到经平移和旋转操作之后的图像矩阵I′；第三步，将图像的大小进行归一化，具体为：去除图像I′中外接矩形之外的部分，将剩余部分用矩阵L表示，将矩阵L归一化为H′×W′，归一化之后的矩阵用N表示；第四步，计算归一化图像的不同阶数的分数傅立叶变换，具体为：令变换阶数a=0.2,0.4,…,1.8，利用快速离散分数傅立叶变换算法计算矩阵N的(a,a)阶二维分数傅里叶变换，得到变换结果其中N(a，a)(u,v)为N的(a,a)阶二维分数傅里叶变换，u=1,2,…H′,v=1,2,…,W′，为虚数单位，exp(.)表示指数函数，|N(a，a)(u,v)|为幅值，表示相位；第五步，舍弃分数傅里叶变换的幅值|N(a，a)(u,v)|，仅保留相位第六步，将归一化图像的各阶分数傅立叶变换的相位直方图作为物体的形状特征，具体为：对于每一个变换阶数a，将量化为20个等级，并计算的直方图，设的直方图为ga(i),其中i＝1,2,…,20表示量化等级,a=0.2,0.4,…,1.8表示变换阶数，将直方图{ga(i)|i＝1,..,20;a＝0.2,0.4...,1.8}作为输入图像矩阵I中的目标的形状特征。2CN102722895A说明书1/2页基于分数傅立叶变换的形状描述方法技术领域[0001]本发明涉及一种形状描述方法，特别是涉及一种数字图像中的形状描述方法。背景技术[0002]目标的形状特征被广泛用于目标识别中，对于物体形状的描述是计算机视觉的重要任务之一。现有的目标形状描述方法可大体上分为两大类：基于边界的形状描述和基于区域的形状描述。其中，基于边界的方法描述目标的形状仅考虑目标边界上的像素点。与之相反，基于区域的方法则从整个目标图像的区域来抽取形状的特征。目前比较常用的基于边界的目标形状描述技术主要有傅里叶描述子、小波描述子、小波-傅里叶描述子等。傅里叶描述子因其计算简单、定义清晰、能量向低频集中的特点，被广泛应用于形状描述领域。傅里叶变换描述子的主要思想是将目标轮廓转化为一维信号，并对此信号进行傅里叶变换，将其从空间域变换到频率域,用图像的频谱特征来描述目标的形状特征。但是传统的傅里叶变换采用全局性的基函数决定其只能用来处理确定的平稳信号，对于时变的非平稳信号则无能为力。[0003]分数傅立叶变换是傅立叶变换的推广形式，它将信号表示为chirp信号的组合。分数傅立叶变换克服了傅立叶变换将时域信息完全摒弃的缺点，通过一种简单的方式实现了信号的从纯粹时间域到纯频率域的全过程的综合描述，能够展示出信号从纯时间域到纯频率域的所有变化特征。目前也有学者尝试用分数傅立叶变换的方法来描述目标的形状