
公开课2.4.1平面向量数量积的物理背景及其含义.ppt

邻家****mk









亲,该文档总共30页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料
2.4.1平面向量数量积的物理背景及其含义.ppt
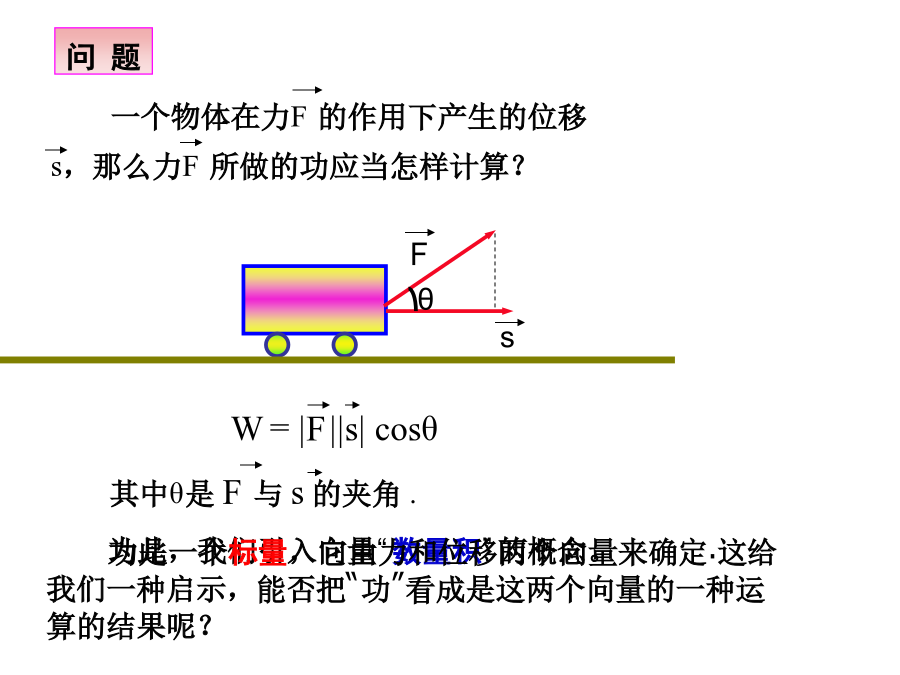
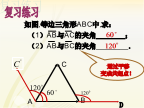
如图,等边三角形ABC中,求:(1)AB与AC的夹角____;(2)AB与BC的夹角________.问题情境:位移S我们将功的运算类比到两个向量的一种运算,得到向量“数量积”的概念。2.4.1平面向量数量积的物理背景及其含义平面向量数量积的定义:注意:注意:练习:课本106页1向量数量积的性质(B1)B向量在方向上的投影是数量,不是向量,什么时候为正,什么时候为负?1.向量a的模为10,它与x轴正方向的夹角为150°,则它在x轴上的投影为()平面向量数量积的运算率:数量积不满足结合律和消去率B1.下列命

公开课2.4.1平面向量数量积的物理背景及其含义.ppt
2.4.1平面向量数量积的物理背景及其含义数乘定义:运算律:向量的夹角问题问题:如果我们将公式中的力与位移类比推广到两个一般向量,其结果又该如何表述?平面向量的数量积的定义思考:向量的数量积是一个数量,那么它什么时候为正,什么时候为负?问题:向量的数量积运算与实数同向量积的线性运算的结果有什么不同?问题:︱a·b︱与︱a︱︱b︱的大小关系如何?为什么?向量数量积的性质例、在△ABC中,求平面向量数量积的几何意义说明:问题:根据投影的概念,数量积a·b=︱a|︱b︱cosθ的几何意义是什么?练一练:⑴交换律

2.4.1平面向量的数量积的物理背景及其含义[1].ppt
2.4.1平面向量数量积的物理背景及其含义向量数量积的物理背景将公式中的力与位移推广到一般向量一、平面向量数量积的定义O二、平面向量数量积的几何意义《非常学案》58页例1向量数量积的性质总结:四、平面向量数量积的运算律⑴交换律:典例解析当堂检测

2.4.1平面向量数量积的物理背景及其含义(1).ppt
2.4.1平面向量数量积的物理背景及其含义设为任意向量,λ,μ为任意实数,则有:①λ(μ)=(λμ)②(λ+μ)=λ+μ③λ()=λ+λ向量的夹角问题问题:如果我们将公式中的力与位移类比推广到两个一般向量,其结果又该如何表述?平面向量的数量积的定义实数同向量积的线性运算的结果是向量两向量的数量积是一个实数,是一个数量例1:已知|a|=5,|b|=4,求a·b①a与b的夹角θ=120°②a∥b③a⊥b平面向量数量积的几何意义说明:⑴交换律:向量运算常用公式练习:已知a、b都是非零向量,且a+3b与7a5b

公开课2.4.1平面向量数量积的物理背景及其含义.ppt
2.4.1平面向量数量积的物理背景及其含义数乘定义:运算律:向量的夹角问题问题:如果我们将公式中的力与位移类比推广到两个一般向量,其结果又该如何表述?平面向量的数量积的定义思考:向量的数量积是一个数量,那么它什么时候为正,什么时候为负?问题:向量的数量积运算与实数同向量积的线性运算的结果有什么不同?问题:︱a·b︱与︱a︱︱b︱的大小关系如何?为什么?向量数量积的性质例、在△ABC中,求平面向量数量积的几何意义说明:问题:根据投影的概念,数量积a·b=︱a|︱b︱cosθ的几何意义是什么?练一练:⑴交换律
