预览加载中，请您耐心等待几秒...

椭圆曲线公钥密码体制ECC.ppt

预览
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10

亲，该文档总共59页，到这已经超出免费预览范围，如果喜欢就直接下载吧～

下载提示 文本预览

如果您无法下载资料，请参考说明：

1、部分资料下载需要金币，请确保您的账户上有足够的金币

2、已购买过的文档，再次下载不重复扣费

3、资料包下载后请先用软件解压，在使用对应软件打开

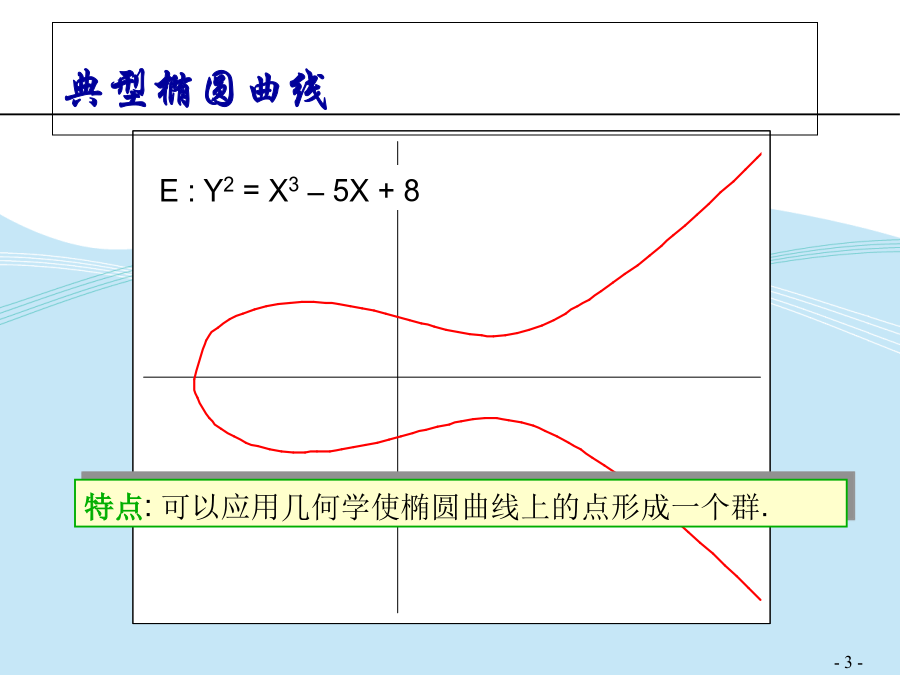
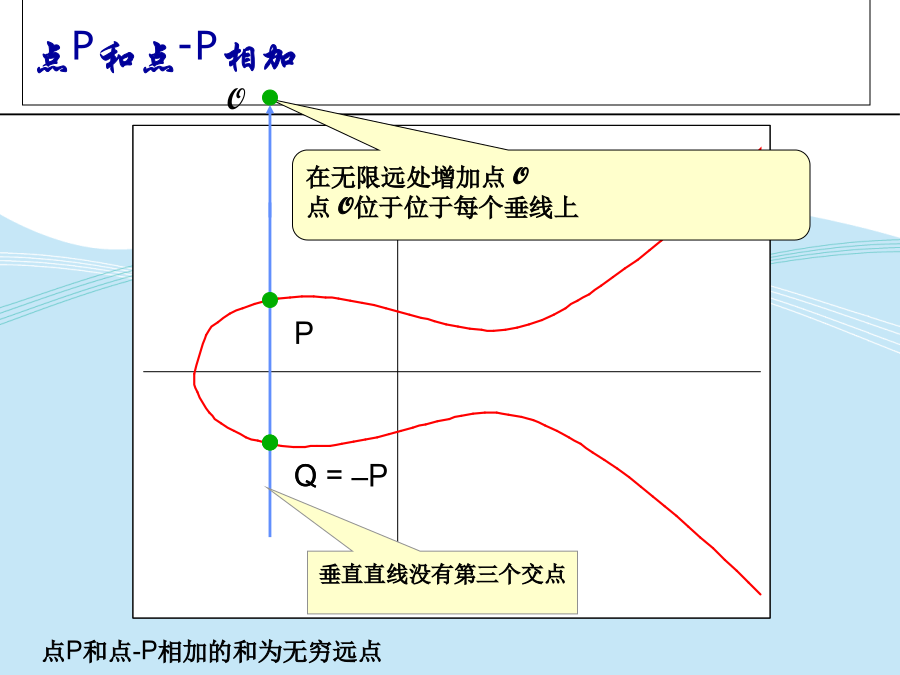
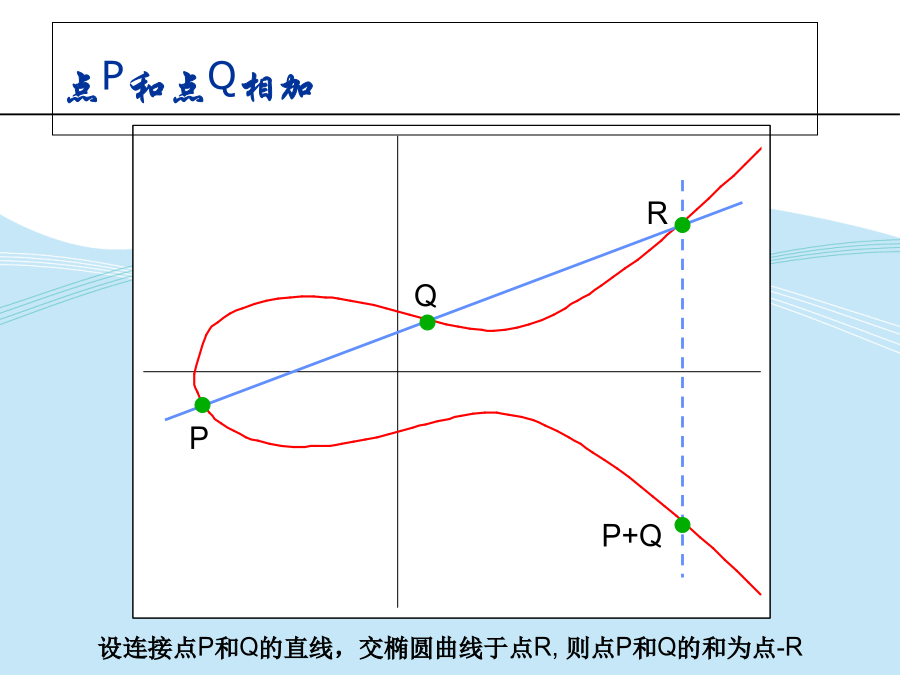
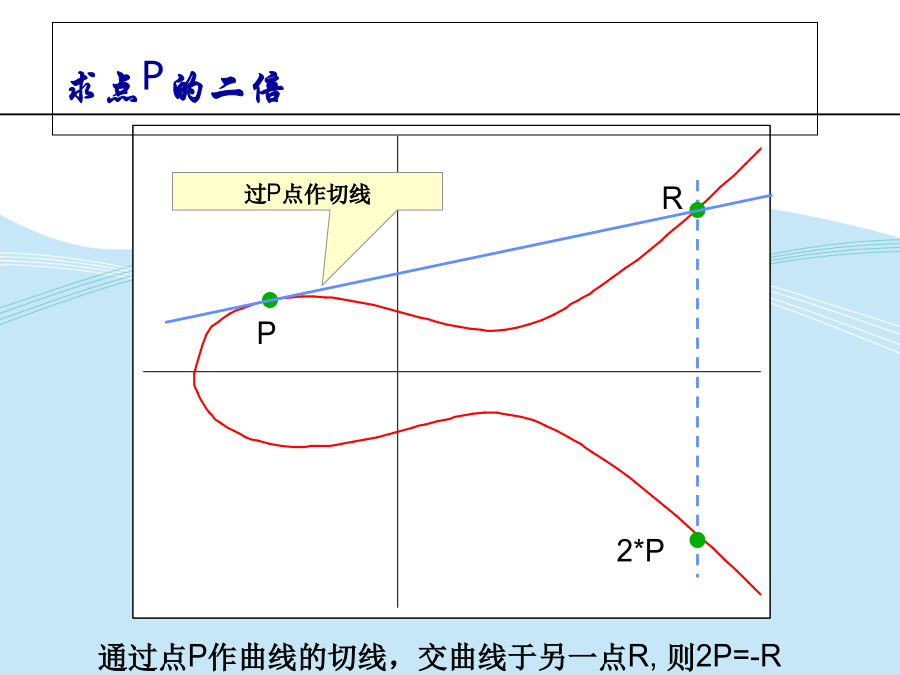
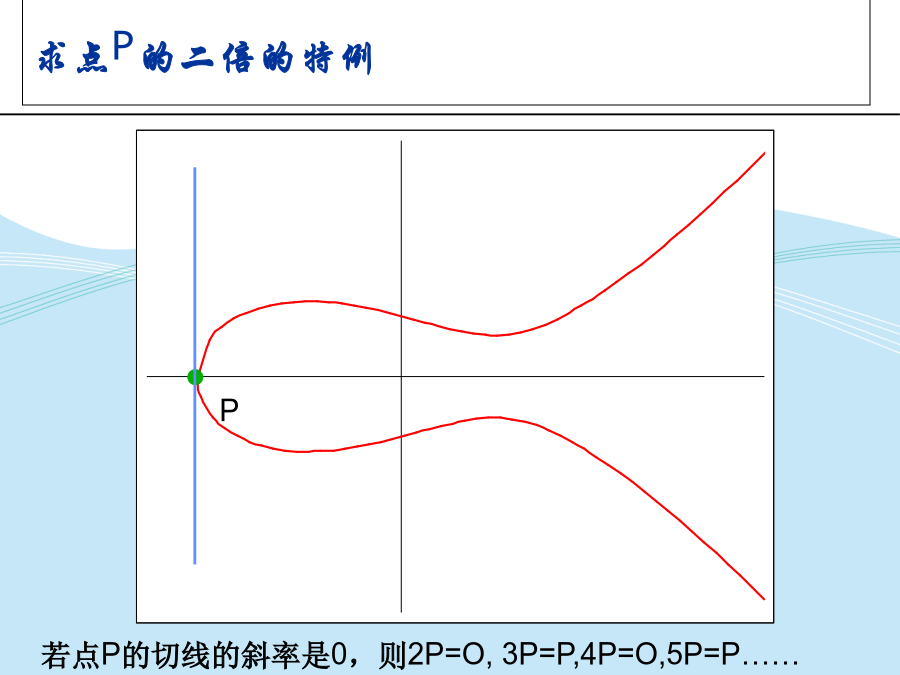
关于椭圆曲线实数域上的椭圆曲线典型椭圆曲线椭圆曲线的加法点P和点-P相加点P和点Q相加求点P的二倍求点P的二倍的特例有限域上的椭圆曲线有限域上的椭圆曲线的点的构造椭圆曲线E23(1,0)的点的构造椭圆曲线E23(1,0)的点的构造有限域上的两个点的加法例题求点P的2倍例题练习上的椭圆曲线上的椭圆曲线举例上的椭圆曲线举例椭圆曲线T=(m=4,f(x)=x4+x+1,g=0010,a=g4,b=g0)的点的构造上椭圆曲线的点的加法逆元上椭圆曲线不同的点的加法运算例题上椭圆曲线的点P的倍点运算例题练习群举例有限域有限域F(p)有限域GF(2m)椭圆曲线群阶(order)椭圆曲线的点的个数练习椭圆曲线的离散对数问题椭圆曲线的离散对数问题的遍历求法群Zp*和E(Fp)的比较ECElGamal加密体制ECElGamal加密体制的加/解密过程举例练习练习密钥长度比较具有128位安全强度的实例：secp256k1具有128位安全强度的实例：sect283k1公钥密码系统中ECC与RSA的对比公钥密码现状下次课再见！