
数值分析9(迭代法收敛性证明)资料.ppt

YY****。。









亲,该文档总共34页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

数值分析9(迭代法收敛性证明)资料.ppt
迭代法收敛性条件迭代误差估计定理总结:例4设||.||为Rn×n上任意一种矩阵范数,则对任意的A∈Rn×n,有AX=b(M–N)X=bMX=NX+b*引理1引理2证:必要性,设迭代法产生的序列{X(k)}收敛,记X*是该序列的极限点,则X*=BX*+f。充分性谱半径小于1是迭代收敛的充要条件,但它不易计算,所以在实际使用中通常并不好用。定理4.2设X*为方程组AX=b的解若||B||<1,则对迭代格式X(k+1)=BX(k)+f有||X(k)–X*||=||(X(k)–X(k+1))+(X(k+1)–

数值分析迭代法的收敛性学习教案.pptx
数值(shùzí)分析迭代法的收敛性一、迭代法的谱半径(bànjìng)性质(xìngzhì):定理:设A为任意n阶方阵,||.||为任意由向量范数诱导(yòudǎo)出的矩阵的范数,则定理(dìnglǐ):设A为n阶方阵,则对任意正数ε,存在一种矩阵范数||.||,使得下面的定理对建立迭代法的收敛条件十分(shífēn)重要.充分性:若二、迭代法的收敛(shōuliǎn)条件证明(zhèngmíng):必要性充分性:若又因为(yīnwèi)推论2:松弛法收敛(shōuliǎn)的必要条件是0<ω<2于是

数值分析31二分法迭代法及收敛性.ppt
3.1.1引言n=1,2时方程的根是大家熟悉的,n=3,4时虽有求根公式但比较复杂,可在数学手册中查到,但已不适合数值计算,而n≥5时就不能用公式表示方程的根.因此,通常对n≥3的多项式方程求根与一般连续函数方程(1.1)一样都可采用迭代法求根.方程f(x)=0的根x*,又称为函数f(x)的零点,它使得f(x*)=0,若f(x)可分解为3.1.2二分法二分法的实施过程如此反复进行,即可的一系列有根区间套若取区间[an,bn]的中点例1用二分法求方程f(x)=x3-x-1=0在(1,1.5)的实根,要求误差

线代迭代法数值分析.pptx
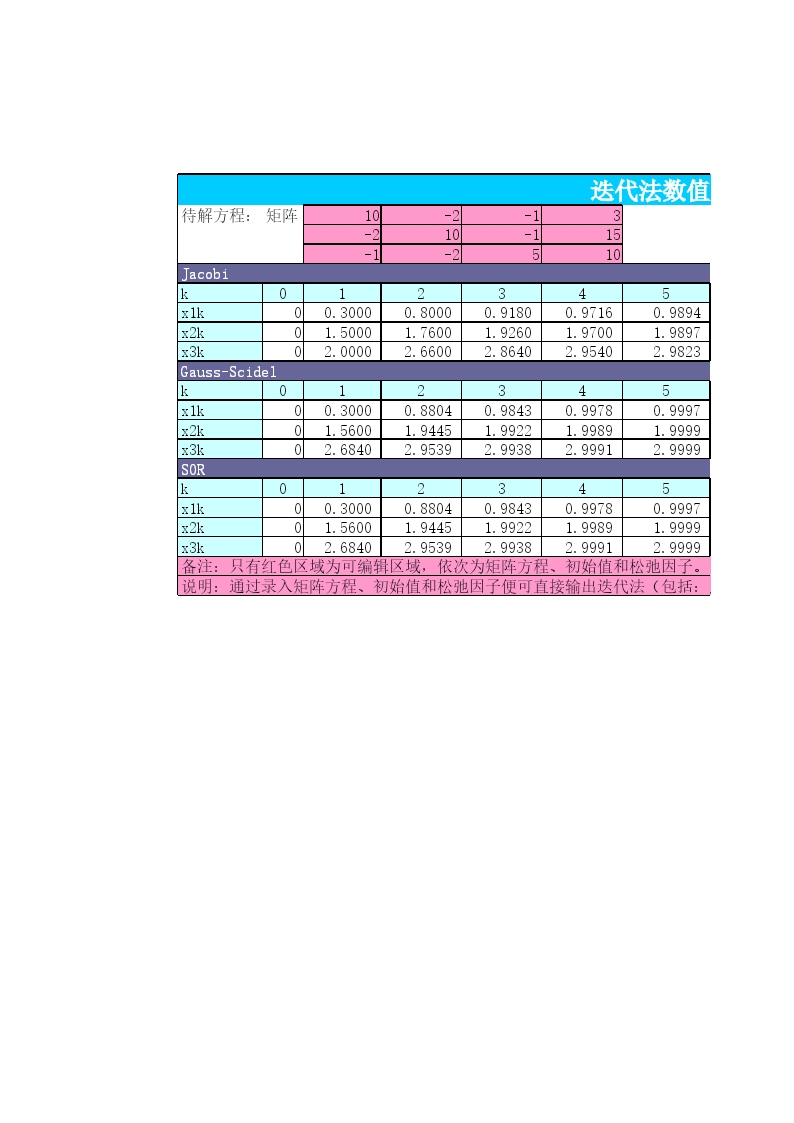
数值分析-迭代法excel版.xls
迭代法数值分析待解方程:矩阵10-2-13初始值:x1=0w=1-210-115x2=0-1-2510x3=0Jacobik012345678910x1k00.30000.80000.91800.97160.98940.99620.99860.99950.99980.9999x2k01.50001.76001.92601.97001.98971.99611.99861.99951.99981.9999x3k02.00002.66002.86402.95402.98232.99382.99772.99922
