
旋转机械振动分析案例.ppt

是你****晨呀






亲,该文档总共49页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

旋转机械振动分析案例.ppt
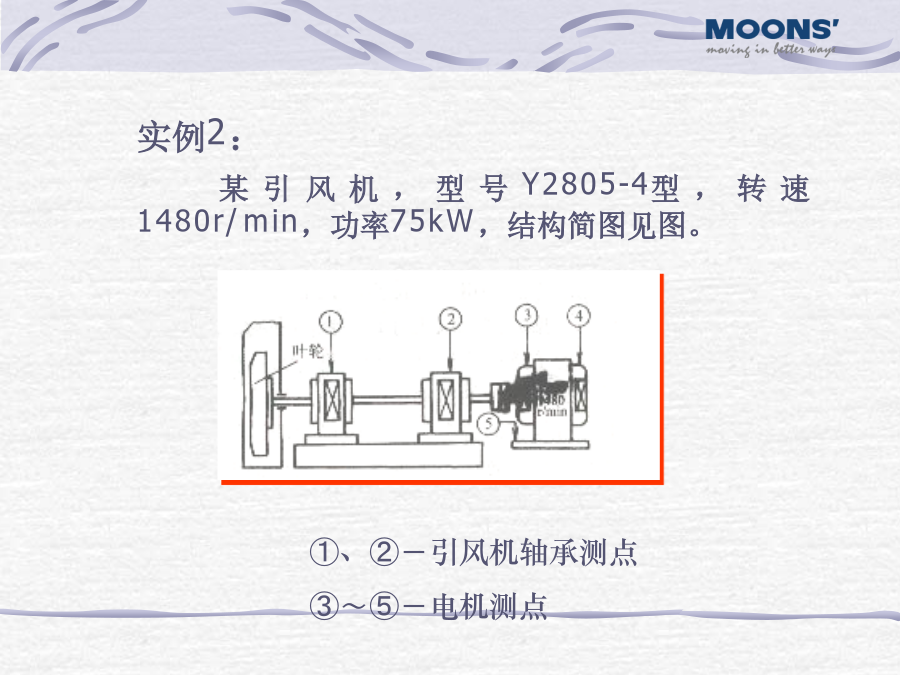
振动分析技术目录:1、旋转机械常见故障的案例分析2、振动故障识别方法转子不平衡产生的原因及频率特征实例1:某公司有一台电动机,额定转速3000r/min,运行中发现振动异常,测取轴承部位的振动信号作频谱分析,其谱图如右下图所示。以电动机转频(50Hz)最为突出,判断电动机转子存在不平衡。在作动平衡测试时,转子不平衡量达5000g.cm,远远超过标准允许值150g.com。经动平衡处理后,振动状态达到正常。这个实例,故障典型,过程完整。它的价值在于印证了不平衡故障的一个最重要特征,激振频率等于转频,又通过动

旋转机械振动分析案例.ppt
振动分析技术目录:1、旋转机械常见故障的案例分析2、振动故障识别方法转子不平衡产生的原因及频率特征实例1:某公司有一台电动机,额定转速3000r/min,运行中发现振动异常,测取轴承部位的振动信号作频谱分析,其谱图如右下图所示。以电动机转频(50Hz)最为突出,判断电动机转子存在不平衡。在作动平衡测试时,转子不平衡量达5000g.cm,远远超过标准允许值150g.com。经动平衡处理后,振动状态达到正常。这个实例,故障典型,过程完整。它的价值在于印证了不平衡故障的一个最重要特征,激振频率等于转频,又通过动

旋转机械振动分析案例.ppt
振动分析技术目录:1、旋转机械常见故障的案例分析2、振动故障识别方法转子不平衡产生的原因及频率特征实例1:某公司有一台电动机,额定转速3000r/min,运行中发现振动异常,测取轴承部位的振动信号作频谱分析,其谱图如右下图所示。以电动机转频(50Hz)最为突出,判断电动机转子存在不平衡。在作动平衡测试时,转子不平衡量达5000g.cm,远远超过标准允许值150g.com。经动平衡处理后,振动状态达到正常。这个实例,故障典型,过程完整。它的价值在于印证了不平衡故障的一个最重要特征,激振频率等于转频,又通过动

旋转机械振动及频谱分析.pdf
振动的基础知识及振动测量状态监测与故障诊断概述简谐振动三要素振动波形频率分析和频谱图旋转机械振动测量框图传感器及其选用基频分量幅值和相位的测量旋转机械的振动图示定转速:波形图、频谱图、http://www.immotor.cn轴心轨迹变转速:波德图和极坐标图、三维频谱图、坎贝尔图、轴心位置图典型机械故障特征及频谱图现场动平衡原理诊断实例状态监测故障诊断和状态监测和故障诊断http://www.immotor.cn什么是状态监测和故障诊断?在设备运行中或在基本不拆卸的情况下,通

旋转机械振动分析与工程应用.pptx
会计学第一节旋转机械油膜振荡故障分析第二节旋转机械汽流激振故障分析第一节旋转机械油膜振荡故障分析图2滑动轴承工作原理图A区内,润滑油从大截面流向小截面,流动过程中润滑油受到挤压作用而产生正压力。B区内,润滑油从小截面流向大截面,流动过程中润滑油受到扩散作用而产生负压力。负压力区内润滑油膜破裂,因此负压不可能存在,实际油压为零。润滑油压周向分布如图2(b)所示。图2(c)给出了轴向润滑油压力分布。中间位置处的油压最大,由中间向两端压力按抛物线规律减小。图2所示的圆柱轴承只含有一个收敛油楔,因此又称单油楔轴承
