
塑性力学-梁的弹塑性弯曲及梁和刚架的塑性极限分析.ppt

音景****ka








亲,该文档总共69页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

塑性力学-梁的弹塑性弯曲及梁和刚架的塑性极限分析.ppt
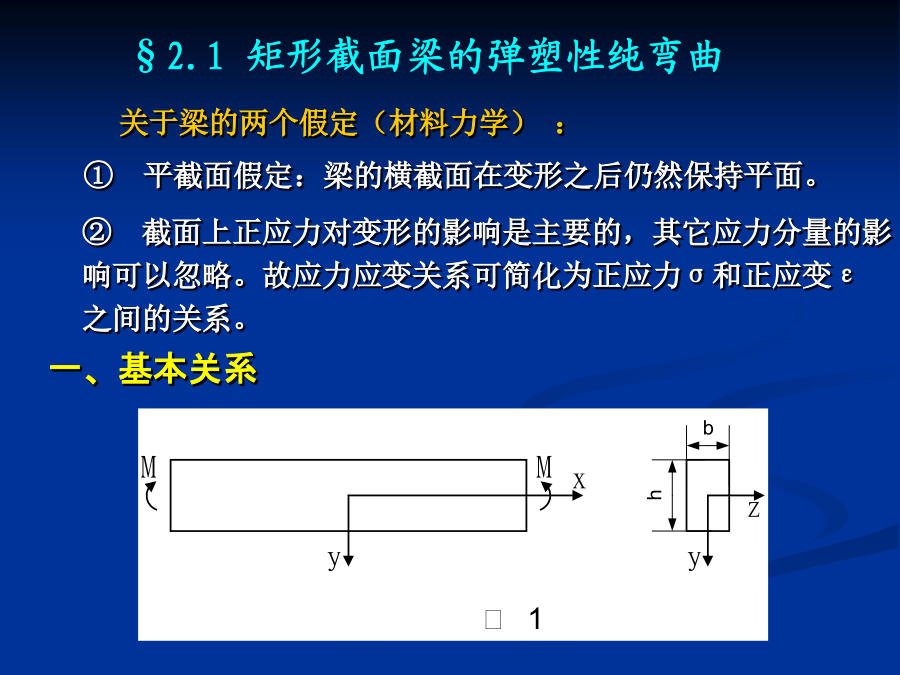
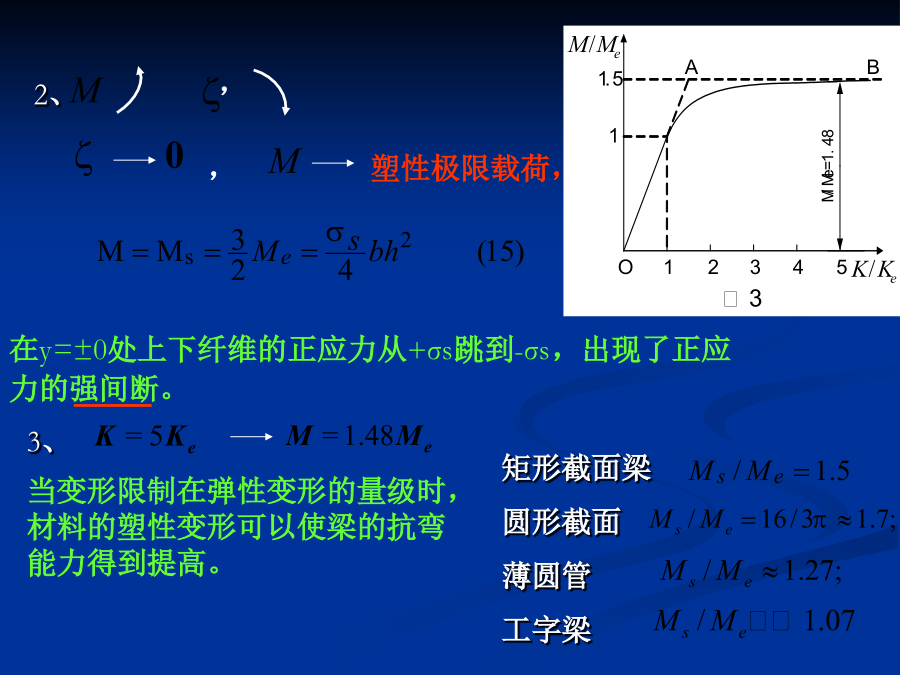
第二章梁的弹塑性弯曲及梁和刚架的塑性极限分析§2.1矩形截面梁的弹塑性纯弯曲考虑梁的纯弯曲问题,故(3)式中轴向力为零,N=0,而(4)式的弯矩M与x无关。在梁的最上层和最下层,应力的绝对值最大,故开始屈服所对应的弯矩和曲率为三、弹塑性阶段或1、表明虽然梁截面的外层纤维已进入塑性屈服阶段,但由于其中间部分仍处于弹性阶段,“平截面”的变形特性限制了外层纤维塑性变形的大小,因而它们是处于约束塑性变形状态,梁的曲率完全由中间弹性部分控制。,三、卸载时的残余曲率和残余应力卸载后的残余曲率与未卸载时的曲率之比:3、

塑性力学-梁的弹塑性弯曲及梁和刚架的塑性极限分析.ppt
第二章梁的弹塑性弯曲及梁和刚架的塑性极限分析§2.1矩形截面梁的弹塑性纯弯曲考虑梁的纯弯曲问题,故(3)式中轴向力为零,N=0,而(4)式的弯矩M与x无关。在梁的最上层和最下层,应力的绝对值最大,故开始屈服所对应的弯矩和曲率为三、弹塑性阶段或1、表明虽然梁截面的外层纤维已进入塑性屈服阶段,但由于其中间部分仍处于弹性阶段,“平截面”的变形特性限制了外层纤维塑性变形的大小,因而它们是处于约束塑性变形状态,梁的曲率完全由中间弹性部分控制。,三、卸载时的残余曲率和残余应力卸载后的残余曲率与未卸载时的曲率之比:3、

塑性力学-梁的弹塑性弯曲及梁和刚架的塑性极限分析.ppt
第二章梁的弹塑性弯曲及梁和刚架的塑性极限分析§2.1矩形截面梁的弹塑性纯弯曲考虑梁的纯弯曲问题,故(3)式中轴向力为零,N=0,而(4)式的弯矩M与x无关。在梁的最上层和最下层,应力的绝对值最大,故开始屈服所对应的弯矩和曲率为三、弹塑性阶段或1、表明虽然梁截面的外层纤维已进入塑性屈服阶段,但由于其中间部分仍处于弹性阶段,“平截面”的变形特性限制了外层纤维塑性变形的大小,因而它们是处于约束塑性变形状态,梁的曲率完全由中间弹性部分控制。,三、卸载时的残余曲率和残余应力卸载后的残余曲率与未卸载时的曲率之比:3、

梁的弹塑性弯曲.ppt
梁的弹塑性弯曲dx3456789101112

梁的弹塑性弯曲.ppt
dx2345678910精品课件!精品课件!13
