位错的应力场与应变场.ppt

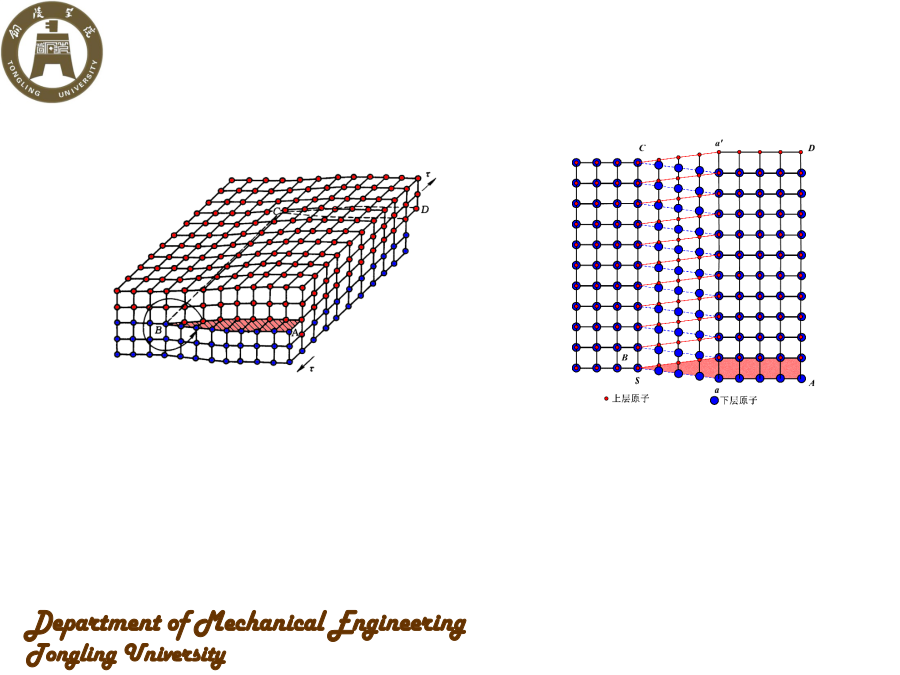
根据几何形态特征，可把晶体缺陷分为三类：
(1)点缺陷、(2)线缺陷、(3)面缺陷

(1)点缺陷：特征是在三维空间的各个方向上的尺寸都很小，亦称为零维缺陷。如空位、间隙原子等。

(2)线缺陷：特征是在两个方向上的尺寸很小，在一个方向上的尺寸较大，亦称为一维缺陷。如晶体中的各类位错。

(3)面缺陷：特征是在一个方向上的尺寸很小，在另外两个方向上的尺寸较大，亦称二维缺陷。如晶界、相界、层错、晶体表面等。刃型位错柏氏矢量的确定
(a)有位错的晶体(b)完整晶体1.4位错的应力场和应变场1.位错的应力场晶体中存在位错时，位错线附近的原子偏离了正常位置，引起点阵畸变，从而产生应力场。在位错的中心部，原子排列特别紊乱，超出弹性变形范围，虎克定律已不适用。中心区外，位错形成的弹性应力场可用各向同性连续介质的弹性理论来处理。分析位错应力场时，常设想把半径约为0.5～1nm的中心区挖去，而在中心区以外的区域采用弹性连续介质模型导出应力场公式。为研究位错应力场问题，一般把晶体分作两个区域：
1）位错中心附近
因畸变严重，须直接考虑晶体结构和原子之间的相互作用。

2）远离位错中心区，
因畸变较小，可简化为连续弹性介质，用线弹性理论进行处理。
位错的畸变：以弹性应力场和应变能的形式表达。一、应力分量：
物体中任意一点的应力状态均可用九个应力分量描述。
用直角坐标方式表达九个应力分量：
正应力分量：σxx、σyy、σzz
切应力分量：τxy、τyz、τzx、τyx、τzy、τxz。用圆柱坐标方式表达九个应力分量：
正应力分量：σrr、σθθ、σzz），
切应力分量：τrθ、τθr、τθz、τzθ、τzr、τrz在平衡条件下，τxy=τyx、τyz=τzy、τzx=τxz
（τrθ=τθr、τθz=τzθ、τzr=τrz），
实际只有六个应力分量就可充分表达一个点的应力状态。与这六个应力分量相应的应变分量：
εxx、εyy、εzz（εrr、εθθ、εzz）和γxy、γyz、γzx（γrθ、γθz、γzr）。
（1）螺型位错的应力场螺型位错的应力场螺位错周围应力分量：由虎克定律得：14（2）刃型位错应力场刃型位错的应力场刃型位错应力场特点：
1）正应力分量与切应力分量同时存在。
2）各应力分量均与z值无关，表明与刃型位错线平行的直线上各点应力状态相同。
3）应力场对称于Y轴（多余半原子面）。4）y＝0时，σxx＝σyy＝σzz＝0，即在滑移面上无正应力，只有切应力，且切应力最大。
5）y＞0时，σxx＜0；y＜0时，σxx＞0，即在滑移面上侧x方向为压应力，而在滑移面下侧x方向为拉应力。
6）x＝y时，σyy及τxy均为零。
正刃型位错周围的应力场
位错周围弹性应力场的存在增加了晶体的能量，这部分能量称为位错的应变能。
位错的应变能：应包括位错中心区应变能E0和位错应力场引起的弹性应变能Ee，即

位错中心区点阵畸变很大，不能用线弹性理论计算E0。
据估计，E0约为总应变能的1/10～1/15左右，故常忽略，而以Ee代表位错的应变能。
位错的应变能：可根据造成这个位错所作的功求得。刃位错的应变能螺位错的应变能比较刃位错应变能和螺位错应变能可看出：

当b相同时，

一般金属泊松比ν＝0.3～0.4，若取ν=1/3，得

即刃位错弹性应变能比螺位错弹性应变能约大50%。一个位错线与其柏氏矢量b成φ角的混合位错，可分解为一个柏氏矢量模为bsinφ的刃位错和一个柏氏矢量模为bcosφ的螺位错。
分别算出两位错分量应变能，其和即为混合位错应变能：

式中称为混合位错角度因素，k≈1～0.75。从以上各应变能的公式可以看出：
1）位错应变能与b2成正比，故柏氏矢量模│b│反映了位错的强度。b越小，位错能量越低，在晶体中越稳定。
为使位错能量最低，柏氏矢量都趋于取密排方向的最小值。

2）当r0→0时应变能无穷大，故在位错中心区公式不适用。

3）r0－位错中心区半径，近似地，r0≈b≈2.5×10-8cm；
R－位错应力场最大作用半径，在实际晶体中，受亚晶界限制，一般取R≈10-4。代入各式，则单位长度位错的应变能公式可简化为：

α是与几何因素有关的系数，均为0.5～１。讨论和练习位错应变能约为其总能量的90%。反映了位错的能量与切变模量成正比，与柏氏矢量的模的平方成反比。练习1已知铜晶体的切变模量G=4×1010Nm-2，位错的柏氏矢量等于原子间距，b=2.5×10-10m，取α=0.75，计算（1）单位长度位错线的应变能。（2）单位体积的严重变形铜晶体内部存储的位错应变能。（设位错密度为1010m/cm3）位错线张力定义:
为使位错线增加一定长度dl所做的功W：

显然，此功应等于位错的应变能：

常取α＝0.5，于是线张力为：

线张力