多址接入信道.ppt

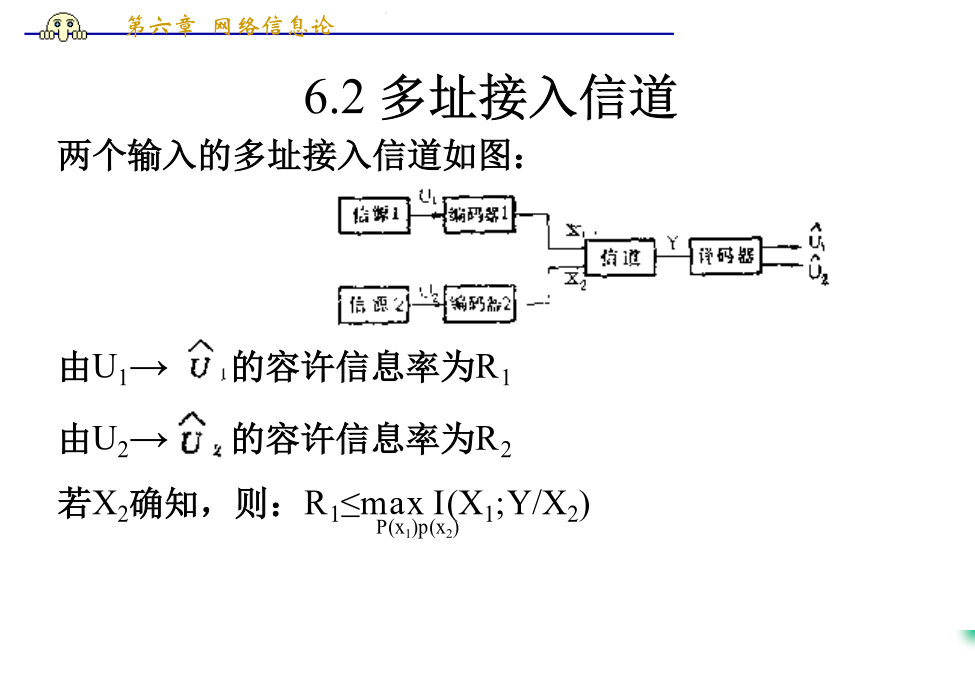
第六章网络信息论6.1通信网信道分类6.2多址接入信道C1＝maxI(X1;Y/X2)
＝max[H(Y/X2)－H(Y/X1X2)]
即R1≤C1
同理：C2＝maxI(X2;Y/X1)

＝max[H(Y/X1)－H(Y/X1X2)]

即R2≤C1
C12＝maxI(X1X2;Y)＝max[H(Y)-Y/X1X2]
显然：(R1+R2)≤C12当X1和X2相互独立时，C1，C2和C12之间必存在
不等式：C12≤C1＋C2
显然，单独传二路的容量大于同时传的容量。
当各信源相互独立时，可推广
得到多址接入信道情况：
分别规定各信源信息率限制：
Rr≤Cr＝maxI(Xr；Y/X1X2‥XN)
联合限制：6.3广播信道R1≤I(U1;Y1)＝I(X;Y1/U2)

R2≤I(U2;Y2)＝I(X;Y2/U1)

R1＋R2≤I(U1U2;Y1Y2)＝I(X;Y1Y2)

6.4相关信源的多用户信道问题由于信源的相关性，必有：
H(X1)+H(X2)≥H(X1X2)
及：H(X1)≥H(X1/X2),H(X2)≥H(X2/X1)
因此，完全无差错地传输信息的充分必要条件：
C1＞H(X1/X2),C2＞H(X2/X1)
C1+C2＞H(X1X2)*
编码器1未知X2情况，却在C1小于H(X1)时还能编出码，并无差错地把X1传送出去，这是由于存在边信息。边信息：若存在一个与X1有关联的随机变量X2，同时送到编码器和译码器，则可对信道要求降低，这种X2所能提供的关于X1的信息称为边信息。

在无X2时，要无差错地传送X1就必须有C>H(X1)；利用X2提供的边信息，只要C>H(X1/X2)即可。研究表明，编码器并不要求X2的具体值，只要知道X2的概率分布和它与X1的关联性，就能按H(X1/X2)来编码，所以对信道的要求是只要能传送H(X1/X2)就可以了。