
《圆和直线的极坐标方程》.ppt

YY****。。









亲,该文档总共36页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

《圆和直线的极坐标方程》.ppt
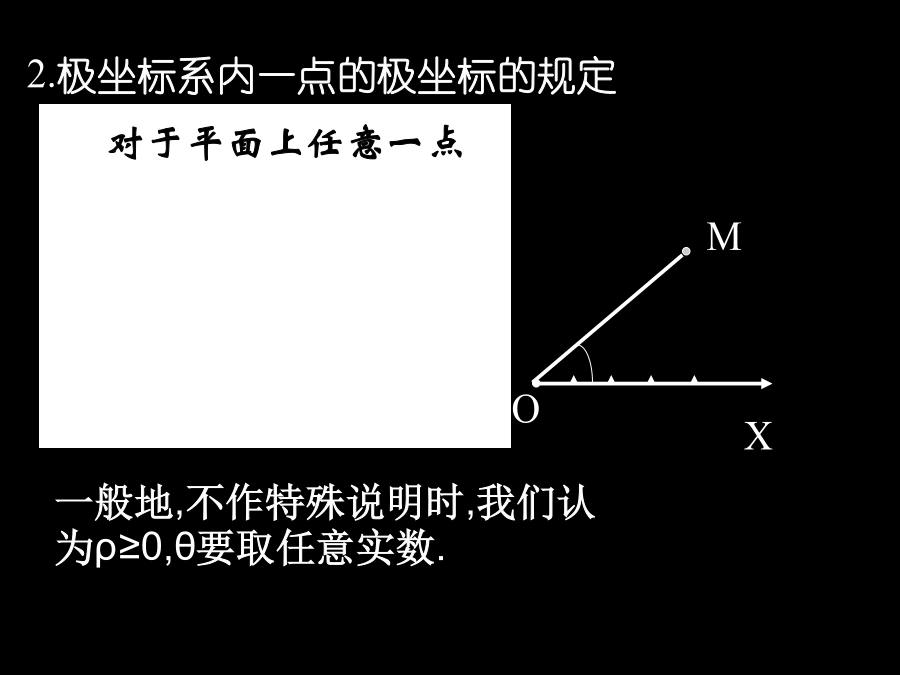
1.圆的极坐标方程1.极坐标系的建立:2.极坐标系内一点的极坐标的规定3.极坐标与直角坐标的互化关系式:曲线的极坐标方程一、定义:如果曲线C上的点与方程f(,)=0有如下关系(1)曲线C上任一点的坐标(所有坐标中至少有一个)符合方程f(,)=0;(2)方程f(,)=0的所有解为坐标的点都在曲线C上。则曲线C的方程是f(,)=0。[探究1]如图,半径为a的圆的圆心坐标为(a,0)(a>0),你能用一个等式表示圆上任意一点的极坐标(,)满足的条件?[探究1]如图,半径为a的圆的圆心坐标为(

圆和直线的极坐标方程.pptx
1.极坐标系的建立:2.极坐标系内一点的极坐标的规定3.极坐标与直角坐标的互化关系式:曲线的极坐标方程一、定义:如果曲线C上的点与方程f(,)=0有如下关系(1)曲线C上任一点的坐标(所有坐标中至少有一个)符合方程f(,)=0;(2)方程f(,)=0的所有解为坐标的点都在曲线C上。则曲线C的方程是f(,)=0。[探究1]如图,半径为a的圆的圆心坐标为(a,0)(a>0),你能用一个等式表示圆上任意一点的极坐标(,)满足的条件?[探究1]如图,半径为a的圆的圆心坐标为(a,0)(a>0)

《圆和直线的极坐标方程》.ppt
1.圆的极坐标方程1.极坐标系的建立:2.极坐标系内一点的极坐标的规定3.极坐标与直角坐标的互化关系式:曲线的极坐标方程一、定义:如果曲线C上的点与方程f(,)=0有如下关系(1)曲线C上任一点的坐标(所有坐标中至少有一个)符合方程f(,)=0;(2)方程f(,)=0的所有解为坐标的点都在曲线C上。则曲线C的方程是f(,)=0。[探究1]如图,半径为a的圆的圆心坐标为(a,0)(a>0),你能用一个等式表示圆上任意一点的极坐标(,)满足的条件?[探究1]如图,半径为a的圆的圆心坐标为(

《圆和直线的极坐标方程》.ppt
1.圆的极坐标方程1.极坐标系的建立:2.极坐标系内一点的极坐标的规定3.极坐标与直角坐标的互化关系式:曲线的极坐标方程一、定义:如果曲线C上的点与方程f(,)=0有如下关系(1)曲线C上任一点的坐标(所有坐标中至少有一个)符合方程f(,)=0;(2)方程f(,)=0的所有解为坐标的点都在曲线C上。则曲线C的方程是f(,)=0。[探究1]如图,半径为a的圆的圆心坐标为(a,0)(a>0),你能用一个等式表示圆上任意一点的极坐标(,)满足的条件?[探究1]如图,半径为a的圆的圆心坐标为(

参数方程、极坐标教案直线和圆的极坐标方程.doc
数学在线网http://www.suniong.com搜集,仅供学习和研究使用!第三章参数方程、极坐标教案直线和圆的极坐标方程教学目标1.理解建立直线和圆的极坐标方程的关键是将已知条件表示成ρ与θ之间的关系式.2.初步掌握求曲线的极坐标方程的应用方法和步骤.3.了解在极坐标系内,一个方程只能与一条曲线对应,但一条曲线即可与多个方程对应.教学重点与难点建立直线和圆的极坐标方程.教学过程师:前面我们学习了极坐标系的有关概念,了解到极坐标系是不同于直角坐标系的另一种坐标系,那么在极坐标系下可以解决点的轨迹问题吗
