
数学模型-层次分析法的基本步骤.ppt

努力****绮亦









亲,该文档总共34页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

数学模型-层次分析法的基本步骤.ppt
表示,如果大石头为单位重量,则有显然,A的各个列向量与w仅相差一个比例因子。一般地,如果一个正互反阵A满足aij·ajk=aik,i,j,k=1,2,…,n(4)则A称为一致性距阵,简称一致阵。(3)式给出的A显然是一致阵。容易证明n阶一致阵A有下列性质。1、A的秩为1,A的唯一非零特征根为n;2、A的任一列(行)向量都是对应于特征根n的特征值。2、心理学家认为,进行成对比较的因素太多,将超出人的判断能力,最多达之7±2范围。如以9个为限,用1-9尺度表示它们之间的差别正合适。3、Saaty曾用1-3,1

数学模型层次分析法的基本步骤1ppt课件.ppt
表示,如果大石头为单位重量,则有显然,A的各个列向量与w仅相差一个比例因子。一般地,如果一个正互反阵A满足aij·ajk=aik,i,j,k=1,2,…,n(4)则A称为一致性距阵,简称一致阵。(3)式给出的A显然是一致阵。容易证明n阶一致阵A有下列性质。1、A的秩为1,A的唯一非零特征根为n;2、A的任一列(行)向量都是对应于特征根n的特征值。2、心理学家认为,进行成对比较的因素太多,将超出人的判断能力,最多达之7±2范围。如以9个为限,用1-9尺度表示它们之间的差别正合适。3、Saaty曾用1-3,1

数模-层次分析法的基本步骤1.ppt
表示,如果大石头为单位重量,则有显然,A的各个列向量与w仅相差一个比例因子。一般地,如果一个正互反阵A满足aij·ajk=aik,i,j,k=1,2,…,n(4)则A称为一致性距阵,简称一致阵。(3)式给出的A显然是一致阵。容易证明n阶一致阵A有下列性质。1、A的秩为1,A的唯一非零特征根为n;2、A的任一列(行)向量都是对应于特征根n的特征值。2、心理学家认为,进行成对比较的因素太多,将超出人的判断能力,最多达之7±2范围。如以9个为限,用1-9尺度表示它们之间的差别正合适。3、Saaty曾用1-3,1

层次分析法的基本步骤和要点.docx
层次分析法的基本步骤和要点结合一个具体例子,说明层次分析法的基本步骤和要点。【案例分析】市政工程项目建设决策:层次分析法问题提出市政部门管理人员需要对修建一项市政工程项目进行决策,可选择的方案是修建通往旅游区的高速路(简称建高速路)或修建城区地铁(简称建地铁)。除了考虑经济效益外,还要考虑社会效益、环境效益等因素,即是多准则决策问题,考虑运用层次分析法解决。1.建立递阶层次结构应用AHP解决实际问题,首先明确要分析决策的问题,并把它条理化、层次化,理出递阶层次结构。AHP要求的递阶层次结构一般由以下三个层
层次分析法的基本原理与步骤.ppt
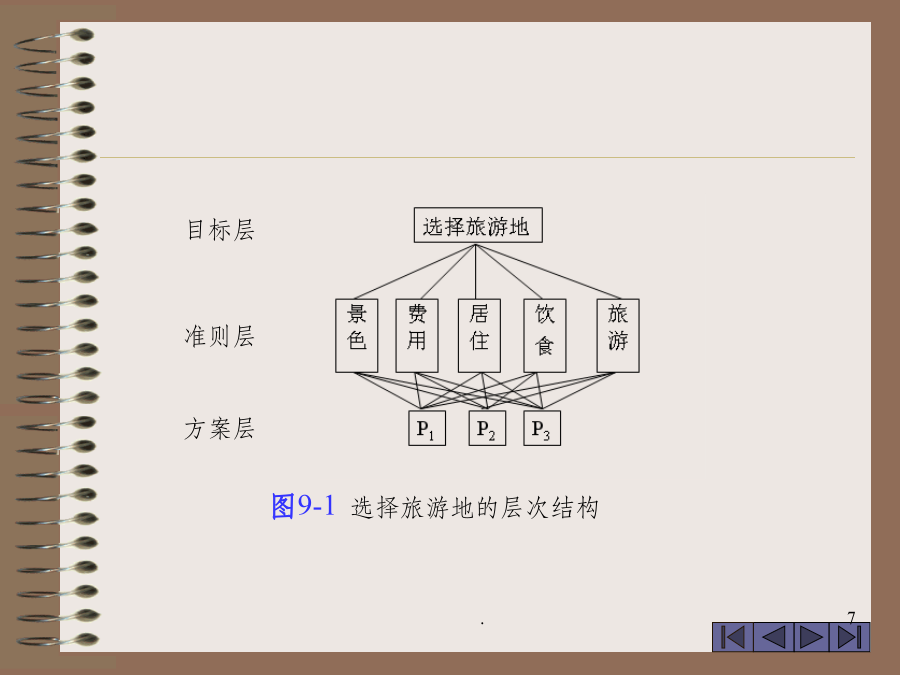
§1层次分析法的基本原理与步骤决策目标例1渡假旅游地的选择标度(aij)比较叛别矩阵的性质比较判别矩阵的一致性可证:W是A的对应特征值n的归一化特征向量(2)和法(4)对数最小二乘法定理2n阶正互反矩阵A的最大特征值max≥n;且当max=n时A是一致的。一致性比率CR一般公式为:W(k)=P(k)P(k-1)…W(2)若CR(k)<0.1,则认为层次结构在第k层水平以上的所有判断具有满意的一致性。B2B5第十三章构造层次结构将数据导出
