
备战2019高考数学大二轮复习专题五立体几何专题能力训练15立体几何中的向量方法理.doc

明轩****la








在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

备战2019高考数学大二轮复习专题五立体几何专题能力训练15立体几何中的向量方法理.doc
专题能力训练15立体几何中的向量方法一、能力突破训练1.如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,点G为AB的中点,AB=BE=2.(1)求证:EG∥平面ADF;(2)求二面角O-EF-C的正弦值;(3)设H为线段AF上的点,且AH=HF,求直线BH和平面CEF所成角的正弦值.2.(2018北京,理16)如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,D,E,F,G分别为AA1,AC,A1C1,BB1的中点,AB=BC=,AC
备战2019高考数学大二轮复习专题五立体几何专题能力训练15立体几何中的向量方法理.doc
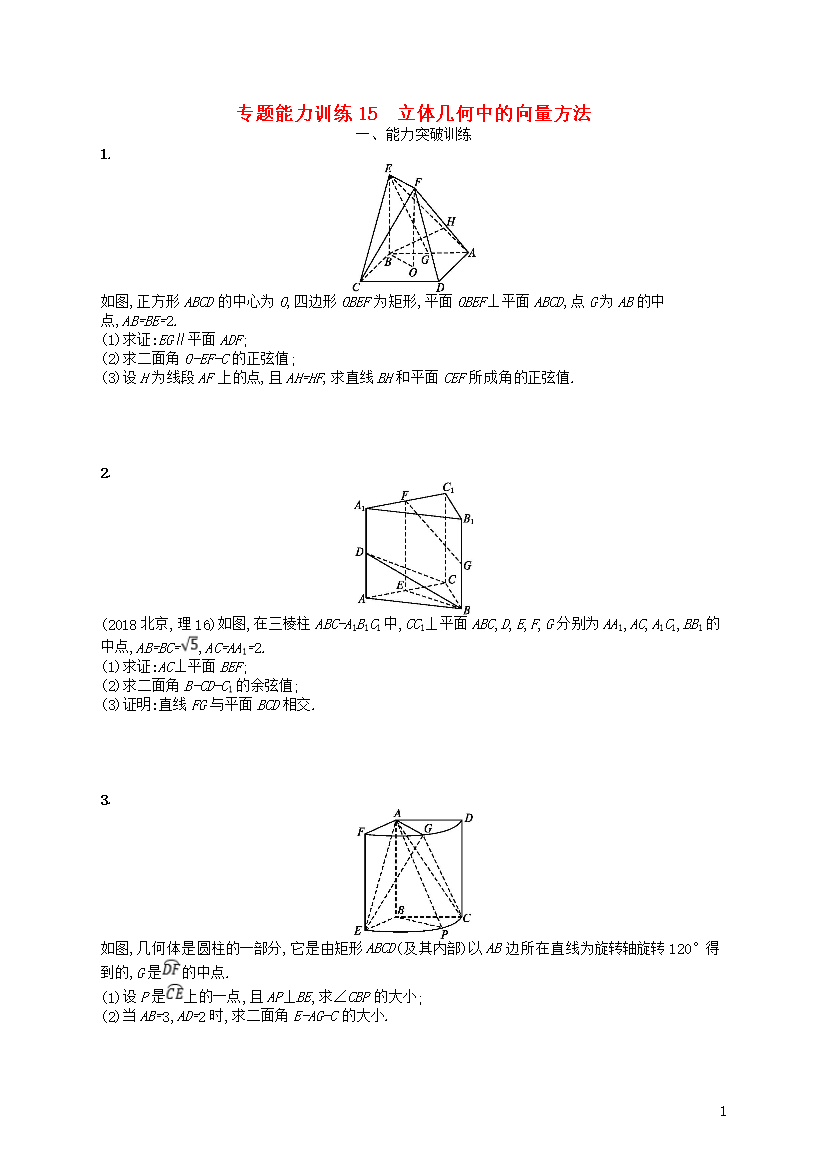
9专题能力训练15立体几何中的向量方法一、能力突破训练1.如图正方形ABCD的中心为O四边形OBEF为矩形平面OBEF⊥平面ABCD点G为AB的中点AB=BE=2.(1)求证:EG∥平面ADF;(2)求二面角O-EF-C的正弦值;(3)设H为线段AF上的点且AH=HF求直线BH和平面CEF所成角的正弦值.2.(2018北京理16)如图在三棱柱ABC-A1B1C1中CC1⊥平面ABCDEFG分别为AA1ACA1C1BB1的中点AB=BC=AC=AA1=2.(1)求证:AC⊥平面BEF;(2)求二面角B-C

备战2019高考数学大二轮复习专题五立体几何专题能力训练15立体几何中的向量方法理.doc
9专题能力训练15立体几何中的向量方法一、能力突破训练1.如图正方形ABCD的中心为O四边形OBEF为矩形平面OBEF⊥平面ABCD点G为AB的中点AB=BE=2.(1)求证:EG∥平面ADF;(2)求二面角O-EF-C的正弦值;(3)设H为线段AF上的点且AH=HF求直线BH和平面CEF所成角的正弦值.2.(2018北京理16)如图在三棱柱ABC-A1B1C1中CC1⊥平面ABCDEFG分别为AA1ACA1C1BB1的中点AB=BC=AC=AA1=2.(1)求证:AC⊥平面BEF;(2)求二面角B-C

备战2019高考数学大二轮复习专题五立体几何专题能力训练15立体几何中的向量方法理.doc
专题能力训练15立体几何中的向量方法一、能力突破训练1.如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,点G为AB的中点,AB=BE=2.(1)求证:EG∥平面ADF;(2)求二面角O-EF-C的正弦值;(3)设H为线段AF上的点,且AH=HF,求直线BH和平面CEF所成角的正弦值.2.(2018北京,理16)如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,D,E,F,G分别为AA1,AC,A1C1,BB1的中点,AB=BC=,AC

备战2019高考数学大二轮复习专题五立体几何专题能力训练15立体几何中的向量方法理.doc
专题能力训练15立体几何中的向量方法一、能力突破训练1.如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,点G为AB的中点,AB=BE=2.(1)求证:EG∥平面ADF;(2)求二面角O-EF-C的正弦值;(3)设H为线段AF上的点,且AH=HF,求直线BH和平面CEF所成角的正弦值.2.(2018北京,理16)如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,D,E,F,G分别为AA1,AC,A1C1,BB1的中点,AB=BC=,AC
