
博弈论的几个经典模型 PPT.ppt

胜利****实阿









亲,该文档总共31页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

博弈论的几个经典模型 PPT.ppt
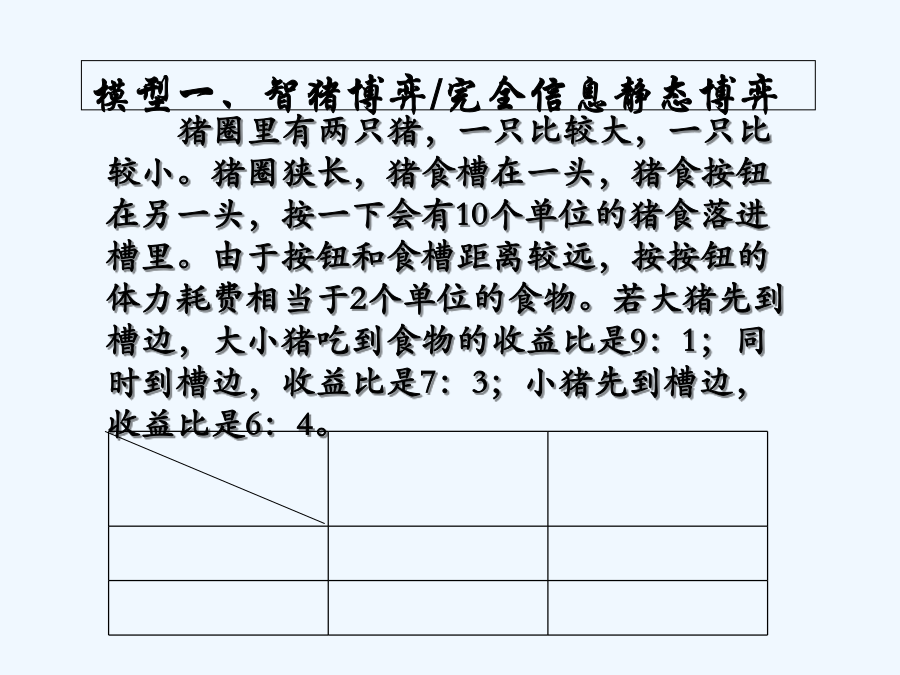
博弈论的几例经典模型引言博弈:game,即是人们遵循一定规则下的活动,参与人的目的是“赢”。进行game的人是很认真的,不同于汉语中游戏的概念。博弈论/对策论:gametheory奥林匹克运动会:OlympicGames。博弈论研究的对象:是理性人或参与者如何选择策略或如何作出行动的决定。理性不一定道德。猪圈里有两只猪,一只比较大,一只比较小。猪圈狭长,猪食槽在一头,猪食按钮在另一头,按一下会有10个单位的猪食落进槽里。由于按钮和食槽距离较远,按按钮的体力耗费相当于2个单位的食物。若大猪先到槽边,大小猪吃

博弈论的几个经典模型-PPT.ppt
博弈论的几例经典模型引言博弈:game,即是人们遵循一定规则下的活动,参与人的目的是“赢”。进行game的人是很认真的,不同于汉语中游戏的概念。博弈论/对策论:gametheory奥林匹克运动会:OlympicGames。博弈论研究的对象:是理性人或参与者如何选择策略或如何作出行动的决定。理性不一定道德。猪圈里有两只猪,一只比较大,一只比较小。猪圈狭长,猪食槽在一头,猪食按钮在另一头,按一下会有10个单位的猪食落进槽里。由于按钮和食槽距离较远,按按钮的体力耗费相当于2个单位的食物。若大猪先到槽边,大小猪吃

博弈论的几个经典模型.ppt
第四章博弈论的几个经典模型引言博弈论的应用领域十分广泛,在经济学、政治科学(国内的以及国际的)、军事战略问题、进化生物学以及当代的计算机科学等领域都已成为重要的研究和分析工具。此外,它还与会计学、统计学、数学基础、社会心理学以及诸如认识论与伦理学等哲学分支有重要联系。按照Aumann所撰写的《新帕尔格雷夫经济学大辞典》“博弈论”辞条的看法,标准的博弈论分析出发点是理性的,而不是心理的或社会的角度。不过,近30年来结合心理学和行为科学、实验经济学的研究成就而对博弈论进行一定改造的行为博弈论(behavoir

博弈论的几个经典模型.ppt
.................................................................................

博弈论的几个经典模型.ppt
第四章博弈论的几个经典模型引言博弈论的应用领域十分广泛,在经济学、政治科学(国内的以及国际的)、军事战略问题、进化生物学以及当代的计算机科学等领域都已成为重要的研究和分析工具。此外,它还与会计学、统计学、数学基础、社会心理学以及诸如认识论与伦理学等哲学分支有重要联系。按照Aumann所撰写的《新帕尔格雷夫经济学大辞典》“博弈论”辞条的看法,标准的博弈论分析出发点是理性的,而不是心理的或社会的角度。不过,近30年来结合心理学和行为科学、实验经济学的研究成就而对博弈论进行一定改造的行为博弈论(behavoir
