
受弯构件梁.ppt

盼易****君a









亲,该文档总共93页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

受弯构件梁.ppt
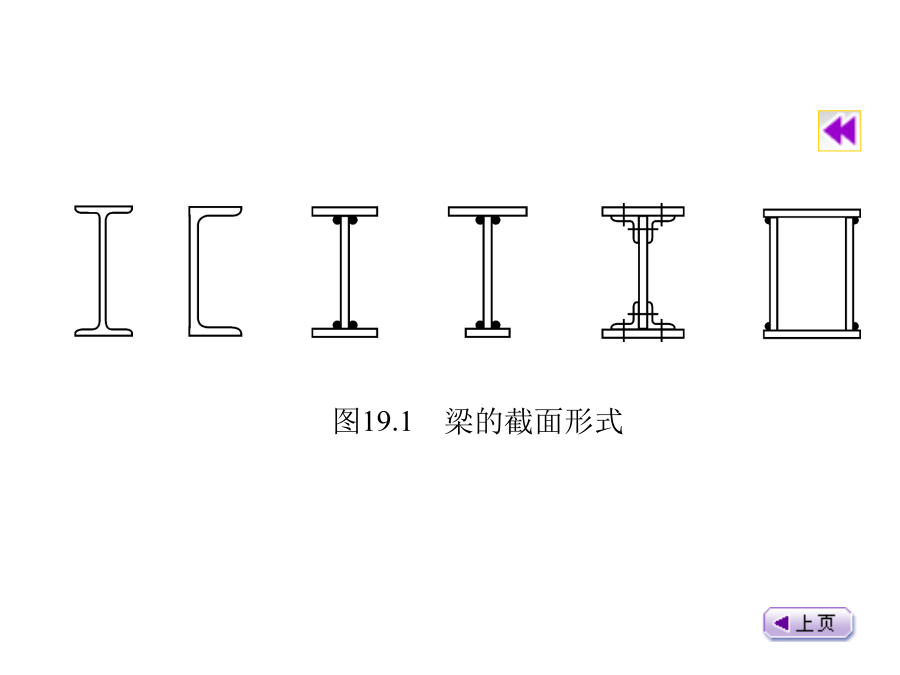
19受弯构件——梁(2)掌握型钢梁和焊接组合梁的截面设计方法;(3)掌握梁腹板和翼缘局部稳定的保证条件和措施,掌握加劲肋的设计方法;(4)掌握梁中各焊缝的计算方法;(5)掌握梁变截面的设计以及梁的构造要求。本章内容19.1概述图19.1梁的截面形式19.2梁的强度、刚度和整体稳定①弹性工作阶段②弹塑性工作阶段③塑性工作阶段把边缘纤维达到屈服点视为梁承载能力的极限状态,作为设计时的依据,叫做弹性设计;在一定的条件下,考虑塑性变形的发展,称为塑性设计。《规范》规定:计算抗弯强度时,对直接承受动力荷载的受弯

受弯构件梁.ppt
19受弯构件——梁(2)掌握型钢梁和焊接组合梁的截面设计方法;(3)掌握梁腹板和翼缘局部稳定的保证条件和措施,掌握加劲肋的设计方法;(4)掌握梁中各焊缝的计算方法;(5)掌握梁变截面的设计以及梁的构造要求。本章内容19.1概述图19.1梁的截面形式19.2梁的强度、刚度和整体稳定①弹性工作阶段②弹塑性工作阶段③塑性工作阶段把边缘纤维达到屈服点视为梁承载能力的极限状态,作为设计时的依据,叫做弹性设计;在一定的条件下,考虑塑性变形的发展,称为塑性设计。《规范》规定:计算抗弯强度时,对直接承受动力荷载的受弯

梁受弯构件.ppt
第一节概述梁主要是用作承受横向荷载的实腹式构件(格构式为桁架),主要内力为弯矩与剪力;梁的正常使用极限状态为控制梁的挠曲变形;梁的承载能力极限状态包括:强度、整体稳定性及局部稳定性;梁的截面主要分型钢与钢板组合截面梁格形式主要有:简式梁格(单一梁)、普通梁格(分主、次梁)及复式梁格(分主梁及横、纵次梁),具体详见P141图5.2第二节梁的强度与刚度弹性最大弯矩塑性铰弯矩截面形状系数梁的《规范》计算方法以部分截面发展塑性(1/4截面)为极限承载力状态单向弯曲双向弯曲式中:γ为塑性发展系数,按P143,表5.

受弯构件梁0.ppt
19受弯构件——梁(2)掌握型钢梁和焊接组合梁的截面设计方法;(3)掌握梁腹板和翼缘局部稳定的保证条件和措施,掌握加劲肋的设计方法;(4)掌握梁中各焊缝的计算方法;(5)掌握梁变截面的设计以及梁的构造要求。本章内容19.1概述图19.1梁的截面形式19.2梁的强度、刚度和整体稳定①弹性工作阶段②弹塑性工作阶段③塑性工作阶段把边缘纤维达到屈服点视为梁承载能力的极限状态,作为设计时的依据,叫做弹性设计;在一定的条件下,考虑塑性变形的发展,称为塑性设计。《规范》规定:计算抗弯强度时,对直接承受动力荷载的受弯
梁板受弯构件计算.pptx
一、受弯构件破坏形式二、梁的截面形式2、截面尺寸◆梁的截面高度与跨度及荷载大小有关。从刚度要求出发,根据设计经验,对一般荷载作用下的梁可参照表3-1初定梁高。◆梁截面宽度b与截面高度的比值b/H,对于矩形截面为1/2~1/2.5,对于T形截面为1/2.5~1/4.◆为了统一模板尺寸和便于施工,梁截面尺寸应按以下要求取值:梁高为200、250、300、350……750、800mm,大于800mm时,以100mm为模数增加。梁宽为120、150、180、200、220、250,大于250mm时,以50mm为模
