
半导体的能带结构-PPT.ppt

文库****坚白









亲,该文档总共116页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

半导体的能带结构-PPT.ppt
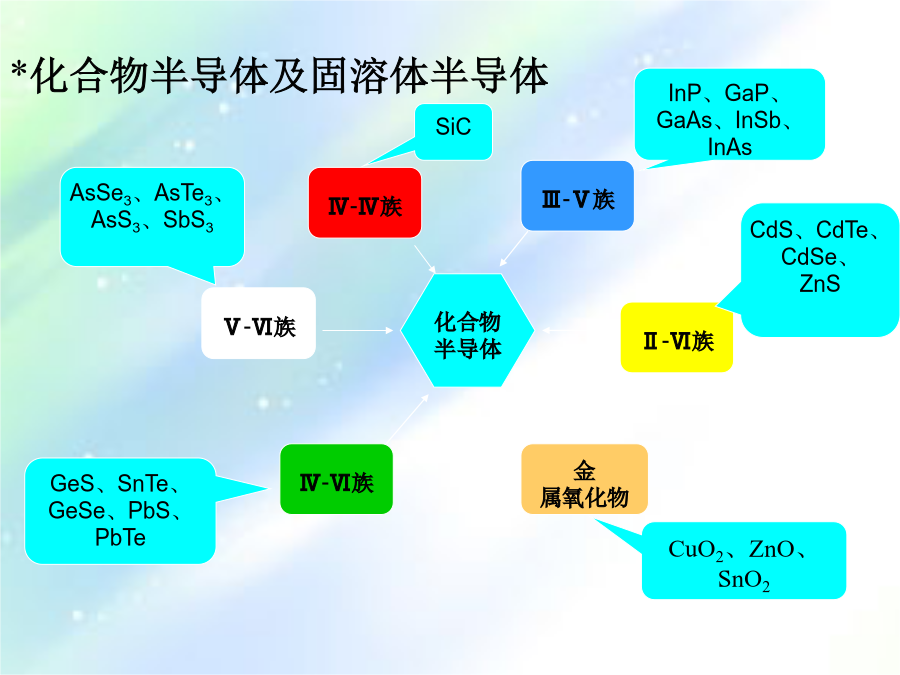
**半导体简介●电阻率导体:ρ<10-3Ωcm例如:ρCu~10-6Ωcm半导体:10-2Ωcm<ρ<109ΩcmρGe=0.2Ωcm绝缘体:ρ>109ΩcmT半导体材料的分类按组成分:*无机半导体晶体材料Ge化合物半导体★过渡金属氧化物半导体:有ZnO、SnO2、V2O5、Cr2O3、Mn2O3、FeO、CoO、NiO等。★尖晶石型化合物(磁性半导体):主要有CdCr2S4、CdCr2Se4、HgCr2S4等。★稀土氧、硫、硒、碲化合物:有EuO、EuS、EuSe、EuTe等。(1)非晶Si、非晶Ge以

半导体的能带结构ppt课件.ppt
**半导体简介●电阻率导体:ρ<10-3Ωcm例如:ρCu~10-6Ωcm半导体:10-2Ωcm<ρ<109ΩcmρGe=0.2Ωcm绝缘体:ρ>109ΩcmT半导体材料的分类按组成分:*无机半导体晶体材料Ge化合物半导体★过渡金属氧化物半导体:有ZnO、SnO2、V2O5、Cr2O3、Mn2O3、FeO、CoO、NiO等。★尖晶石型化合物(磁性半导体):主要有CdCr2S4、CdCr2Se4、HgCr2S4等。★稀土氧、硫、硒、碲化合物:有EuO、EuS、EuSe、EuTe等。(1)非晶Si、非晶Ge以

半导体的能带结构.ppt
**半导体简介●电阻率导体:ρ<10-3Ωcm例如:ρCu~10-6Ωcm半导体:10-2Ωcm<ρ<109ΩcmρGe=0.2Ωcm绝缘体:ρ>109ΩcmT半导体材料的分类按组成分:*无机半导体晶体材料Ge化合物半导体★过渡金属氧化物半导体:有ZnO、SnO2、V2O5、Cr2O3、Mn2O3、FeO、CoO、NiO等。★尖晶石型化合物(磁性半导体):主要有CdCr2S4、CdCr2Se4、HgCr2S4等。★稀土氧、硫、硒、碲化合物:有EuO、EuS、EuSe、EuTe等。(1)非晶Si、非晶Ge以

半导体的能带结构.ppt
**半导体简介●电阻率导体:ρ<10-3Ωcm例如:ρCu~10-6Ωcm半导体:10-2Ωcm<ρ<109ΩcmρGe=0.2Ωcm绝缘体:ρ>109ΩcmT半导体材料的分类按组成分:*无机半导体晶体材料Ge化合物半导体★过渡金属氧化物半导体:有ZnO、SnO2、V2O5、Cr2O3、Mn2O3、FeO、CoO、NiO等。★尖晶石型化合物(磁性半导体):主要有CdCr2S4、CdCr2Se4、HgCr2S4等。★稀土氧、硫、硒、碲化合物:有EuO、EuS、EuSe、EuTe等。(1)非晶Si、非晶Ge以

半导体能带结构.ppt
7、半导体的能带结构或在讨论本征吸收时,光子的动量可以略去,因为本征吸收光子的波矢为104cm-1,而在能带论中布里渊区的尺度为2π/晶格常数,数量级是108cm-1,因此本征光吸收中,因此光吸收的跃迁选择定则可以近似写成但是声子能量是较小的,数量级为百分之几电子伏以下,因此近似的有电子能量差=光子能量在实际的半导体材料中,总是不可避免地存在有杂质和各种类型的缺陷.特别是在半导体的研究和应用中,常常有意识的加入适当的杂质.这些杂质和缺陷产生的附加势场,有可能使电子和空穴束缚在杂质和缺陷的周围,产生局域化的
