预览加载中，请您耐心等待几秒...

随机过程马氏过程.ppt

预览
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10

亲，该文档总共23页，到这已经超出免费预览范围，如果喜欢就直接下载吧～

下载提示 文本预览

如果您无法下载资料，请参考说明：

1、部分资料下载需要金币，请确保您的账户上有足够的金币

2、已购买过的文档，再次下载不重复扣费

3、资料包下载后请先用软件解压，在使用对应软件打开

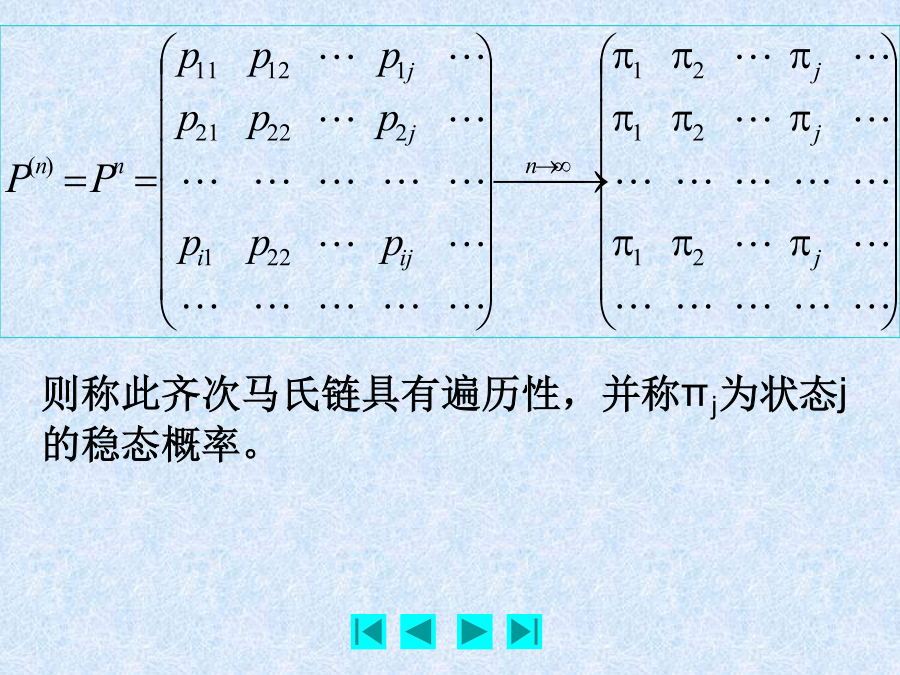
§6.4转移概率的遍历性与平稳分布又如一齐次马氏链，状态空间为E={1,2,3}，其一步转移概率矩阵,二步,三步转移概率矩阵为因此,一般来说，通常讨论关于齐次马氏链的n步转移概率的两方面问题，一是其极限是否存在？二是如果此极限存在，那么它是否与现在所处状态i无关，在马氏链理论中，有关这两方面问题的定理，统称为遍历性定理。则称此齐次马氏链具有遍历性，并称πj为状态j的稳态概率。及概率分布条件解：注意到故由定义4.1知，此链不具有遍历性,也不存在稳态概率。例4.3已知{X(n),n≥0}的初始分布为即此初始分布满足定义4.2中条件，故具有上述转移概率的齐次马氏链为一平稳齐次马氏链，初始分布为其一个平稳分布。由此可见，当我们能判定齐次马氏链的初始分布是一平稳分布时，则该马氏链在任何时刻的绝对概率分布都与初始分布相同。事实上，平稳分布就是不因转移步数变化而改变的分布。此时马氏链处于状态j的概率与时间推移无关，即具有平稳性。可见其平稳分布是存在的，且具有无穷多个.