向量和矩阵的定义和运算专题培训课件.ppt

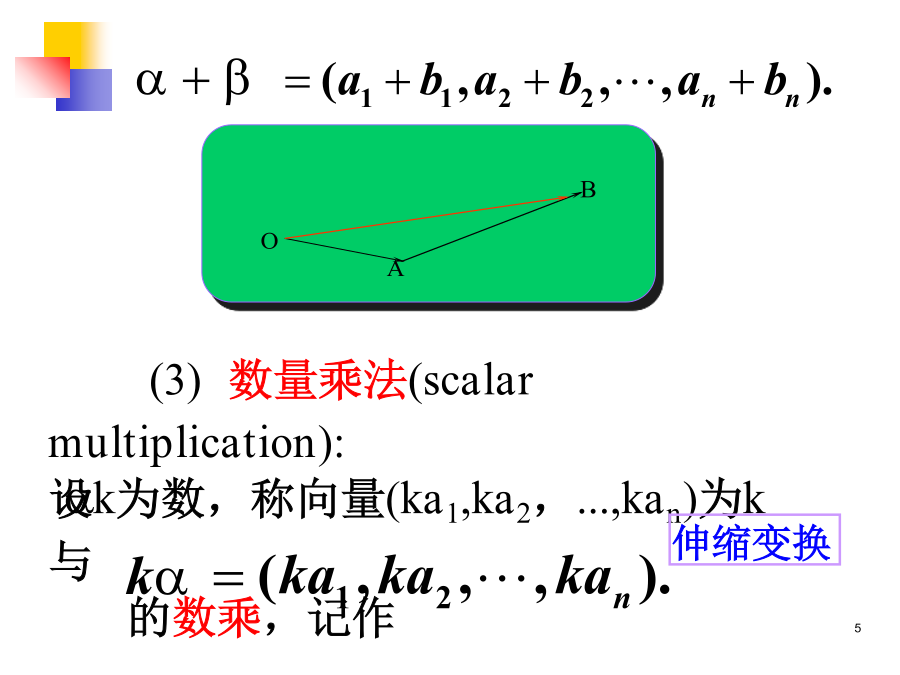
向量和矩阵的定义和运算PPT讲座§1.1向量与矩阵的定义及运算并称数ai为的第i个分量(i=1,2,...,n).定义2设两个n维向量+(4)分量全为零的向量(0,...,0)称为零向
量，记作0.注意:在上面的八条运算规律中只利用
了向量的加法和数乘.但是,利用负向量
的概念,依然可以定义向量的减法运算:例1题中的可以表示为的
形式,称可由向量线性表出,
或称是的一个线性组合.是向量组也即是二、矩阵引例1某商场9月份电视机销售统计表引例2线性方程组定义4数域P中sn个数排成的s行n列的长方形数表元素是实数的矩阵称为实矩阵，元素是复数的矩阵称为复矩阵.本书中讨论的矩阵如不特别声明，都是指实矩阵.一些特殊的矩阵：2.零矩阵：所有元素都为零的矩阵称
为零矩阵,记为0.
注意：不同阶的零矩阵不同.4.对角矩阵：除主对角线上元素外，其它元素都为零的n阶方阵.
(i.e.aij=0,i≠j)5.单位矩阵：若对角线元素为1，其它元素为零的矩阵，称为n阶单位矩阵(identitymatrix),记为En(或In),简记为E.6.数量矩阵：若对角线元素为k(k为常数),其余元素都为零的n阶矩阵，称为n阶数量矩阵(scalarmatrix)，记为kE.矩阵的线性运算(2)加法：称矩阵(3)数量乘法：设k为数域P中的数，
称矩阵(4)负矩阵:将矩阵A=(aij)s×n的各元素取相反符号，得到的矩阵称为矩阵A的负矩阵，记为－A.即矩阵的线性运算性质28解：由等式可得例5设A=(aij)2×3,Eij表示第i行第j列元
素为1，其余元素为0的2×3矩阵
(i=1,2;j=1,2,3),如当两个求和指标独立取值时,连加号的顺序可以交换.引例引例(续)引例(续)设A=(aij)s×n是一个s×n矩阵，B=(bij)n×m是一个n×m矩阵,A的列数等于B的行数.
用cij表示A的第i行与B的第j列的对应分量乘积之和，称矩阵C=(cij)s×m为矩阵A与B的乘积，记为C=AB.注意：(1)只有当第一个矩阵的列数等于第二个矩阵的行数时，两个矩阵才能相乘.例设故例7设例8设仔细观察，我们发现：矩阵的乘法性质(加乘分配律)(双重连加号交换次序)=(A的第i行)(BC的第t列)(2)k(AB)=(kA)B=A(kB),k是一个数；(6)设A为n阶方阵，由乘法结合律，
可定义A的乘幂.规定一些特殊矩阵的乘法练习：设A=(aij)n为任意n阶方阵，D=(dij)n为n阶对角阵,求B=AD,C=DA.52上三角矩阵：如果A=(aij)n的元素aij=0，i>j,i,j=1,2,...,n,则称A为上三角
形矩阵，简称为上三角矩阵.下三角矩阵：如果A=(aij)n的元素aij=0,i<j,i,j=1,2,...,n,则称A为下三角
形矩阵，简称为下三角矩阵.设A=(aij)n，B=(bij)n为上三角矩阵，求C=AB.当i<j时，解:设则由(E+B)X=X(E+B)当且仅当
X+BX=X+XB,
于是AX=XA当且仅当XB=BX,从而有由矩阵的相等得到线性方程组，解之得解：事实上例10设例11设n阶方阵A满足关系式不妨假设B=aA+bE,其中参数a,b应满足例例：设矩阵解：根据可交换的定义，有68类似的,b21=0;b23=0;b31=0;b32=0.
而b11a1=b11a1,可知b11为任意数，
类似的，b22，b33可以任意数.比较：在数的乘法中，若
ac=ad，且a0c=d
(消去律成立)