
弹塑性力学课件-塑性基本概念.ppt

lj****88








亲,该文档总共35页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

弹塑性力学课件-塑性基本概念.ppt
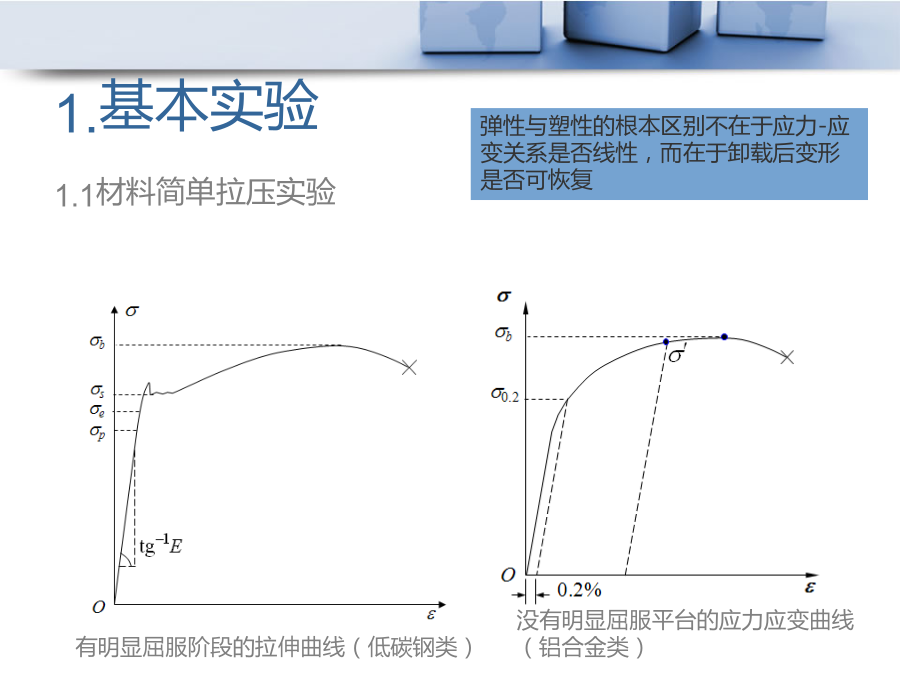
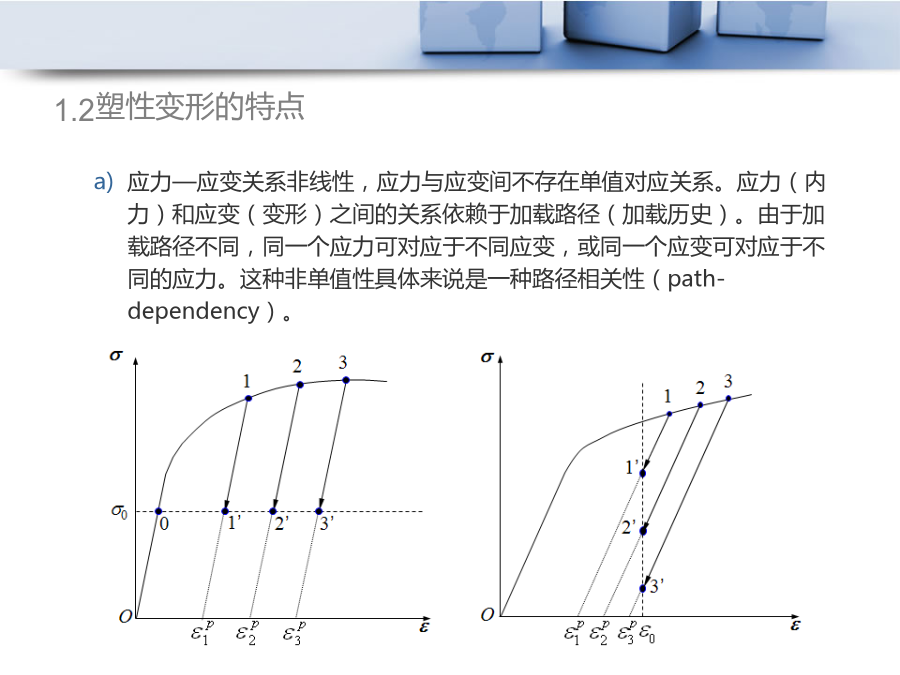
塑性基本概念1.基本实验应力降到零点后继续卸载(压缩),称为反向加载。反向(压缩)屈服、屈服点降低,称为包辛格效应(Bauschinger'seffect),塑性变形使材料出现各向异性。这表明材料的后继屈服性质不仅与它所经历的塑性变形的大小密切相关,还受到它所经历过的塑性变形的方向影响1.2塑性变形的特点由于塑性应变不可恢复,所以外力所作的塑性功具有不可逆性,或称为耗散性(dissipation)。在一个加载-卸载的循环中外力作功恒大于零,这一部分能量被材料的塑性变形损耗掉了。当受力固体产生塑性变形时,将

弹塑性力学课件-塑性基本概念.ppt
塑性基本概念1.基本实验应力降到零点后继续卸载(压缩),称为反向加载。反向(压缩)屈服、屈服点降低,称为包辛格效应(Bauschinger'seffect),塑性变形使材料出现各向异性。这表明材料的后继屈服性质不仅与它所经历的塑性变形的大小密切相关,还受到它所经历过的塑性变形的方向影响1.2塑性变形的特点由于塑性应变不可恢复,所以外力所作的塑性功具有不可逆性,或称为耗散性(dissipation)。在一个加载-卸载的循环中外力作功恒大于零,这一部分能量被材料的塑性变形损耗掉了。当受力固体产生塑性变形时,将

弹塑性力学塑性基本概念ppt课件.ppt
塑性基本概念1.基本实验应力降到零点后继续卸载(压缩),称为反向加载。反向(压缩)屈服、屈服点降低,称为包辛格效应(Bauschinger'seffect),塑性变形使材料出现各向异性。这表明材料的后继屈服性质不仅与它所经历的塑性变形的大小密切相关,还受到它所经历过的塑性变形的方向影响1.2塑性变形的特点由于塑性应变不可恢复,所以外力所作的塑性功具有不可逆性,或称为耗散性(dissipation)。在一个加载-卸载的循环中外力作功恒大于零,这一部分能量被材料的塑性变形损耗掉了。当受力固体产生塑性变形时,将

弹塑性力学精-塑性基本概念ppt课件.ppt
塑性基本概念1.基本实验应力降到零点后继续卸载(压缩),称为反向加载。反向(压缩)屈服、屈服点降低,称为包辛格效应(Bauschinger'seffect),塑性变形使材料出现各向异性。这表明材料的后继屈服性质不仅与它所经历的塑性变形的大小密切相关,还受到它所经历过的塑性变形的方向影响1.2塑性变形的特点由于塑性应变不可恢复,所以外力所作的塑性功具有不可逆性,或称为耗散性(dissipation)。在一个加载-卸载的循环中外力作功恒大于零,这一部分能量被材料的塑性变形损耗掉了。当受力固体产生塑性变形时,将

弹塑性力学-弹塑性本构关系PPT课件.ppt
附加应力对附加应变负做功,即(2)德鲁克塑性公设的表述在应力循环中,外载所作的功为:(3)德鲁克塑性公设的重要推论1屈服曲面的外凸性2塑性应变增量向量与屈服面法向平行3德鲁克塑性公设的评述(4)德鲁克公设的适用条件:①ij0在塑性势面与屈服面之内时,德鲁克公设成立;②ij0在塑性势面与屈服面之间时,德鲁克公设不成立;3.1.3依留申塑性公设的表述残余应力增量与塑性应变增量存在关系:由图(a)可知,对于弹性性质不随加载面改变的非耦合情况,外部作用在应变循环内做功WI和应力循环所作的外部功之间仅差一个正的
