
二次函数y=axh2的图象和性质ppt课件.ppt

lj****88










亲,该文档总共23页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

二次函数y=axh2的图象和性质ppt课件.ppt
二次函数y=a(x-h)2的图象与性质y=ax2y=ax2+k画出二次函数的图像,并说出它们的开口方向、对称轴和顶点.与抛物线顶点(0,0)在同一坐标系中观察和的函数图象,回答问题。图象是轴对称图形对称轴是平行于y轴的直线:x=1.在对称轴(直线:x=1)左侧(即x<1时),函数y=3(x-1)2的值随x的增大而减少,.当a>0时,开口向上;3.抛物线y=ax2+k有如下特点:y=a(x-h)2抛物线2、若将抛物线y=-2(x-2)2的图象的顶点移到原点,则下列平移方法正确的是()A、向上平移2个单位B、

-二次函数y=ax+c的图象和性质ppt课件.ppt
y=ax2例1在同一直角坐标系中,画出二次函数y=x2+1,y=x2-1的图象。讨论讨论把抛物线y=2x2向上平移5个单位,会得到哪条抛物线?向下平移3.4个单位呢?1想一想总结y=ax2+k(1)抛物线y=ax2+c与y=-5x2的形状大小,开口方向都相同,且其顶点坐标是(0,3),则其表达式为,它是由抛物线y=-5x2向平移个单位得到的.练习:5.(1)抛物线y=−2x2+3的顶点坐标是,对称轴是,在___侧,y随着x的增大而增大;在侧,y随着x的增大而减小,当x=_____时,函数y的值最大,最大值

二次函数y_a2+c_的图象和性质课件PPT.ppt
26.1二次函数(3)y=ax21、函数y=2x2的图象的开口,对称轴,顶点是;例2.在同一直角坐标系中,画出二次函数y=x2+1和y=x2-1的图像(1)抛物线y=x2+1,y=x2-1的开口方向、对称轴、顶点各是什么?(2)抛物线y=x2+1,y=x2-1与抛物线y=x2的异同点:总结归纳把抛物线y=2x2向上平移5个单位,会得到那条抛物线?向下平移3.4个单位呢?例题2抛物线y=ax2+k与y=-5x2的形状大小,开口方向都相同,且其顶点坐标是(0,3),则其表达式为,它是由抛物线y=-5x2向平移
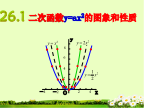
二次函数y=ax2的图象和性质.1.2 二次函数y=ax2的图象和性质》课件.ppt
x复习xxx当x<0(在对称轴的左侧)时,y随着x的增大而减小.当x<0(在对称轴的左侧)时,y随着x的增大而增大.例题与练习1探究归纳1、根据左边已画好的函数图象填空:(1)抛物线y=2x2的顶点坐标是,对称轴是,在侧,y随着x的增大而增大;在侧,y随着x的增大而减小,当x=时,函数y的值最小,最小值是,抛物线y=2x2在x轴的方(除顶点外)。例题与练习思考题已知抛物线y=ax2经过点A(-2,-8)(1)求此抛物线的函数解析式;(2)判断点B(-1,-4)是否在此抛物线上。y=ax2(a≠0)1.抛物

二次函数y=ax2的图象和性质ppt.1.2-二次函数y=ax2的图象和性质.ppt
二次函数图像(1)一般地,形如y=ax2+bx+c(a、b、c为常数,a≠0)的函数,叫做二次函数.其中,x是自变量,a,b,c分别是函数解析式的二次项系数、一次项系数和常数项.xx下面是两个同学画的y=0.5x2和y=-0.5x2的图象,你认为他们的作图正确吗?为什么?xxx共同点:1函数y=-x2,y=-2x2的图像与y=-x2的图像相比,有什么共同点和不同点?1、抛物线y=ax2的顶点是原点,对称轴是y轴。1思考:在同一坐标系内,抛物线y=x2与抛物线y=-x2的位置有什么关系?一般地,抛物线y=a
