运筹学-单纯形法1ppt课件.ppt

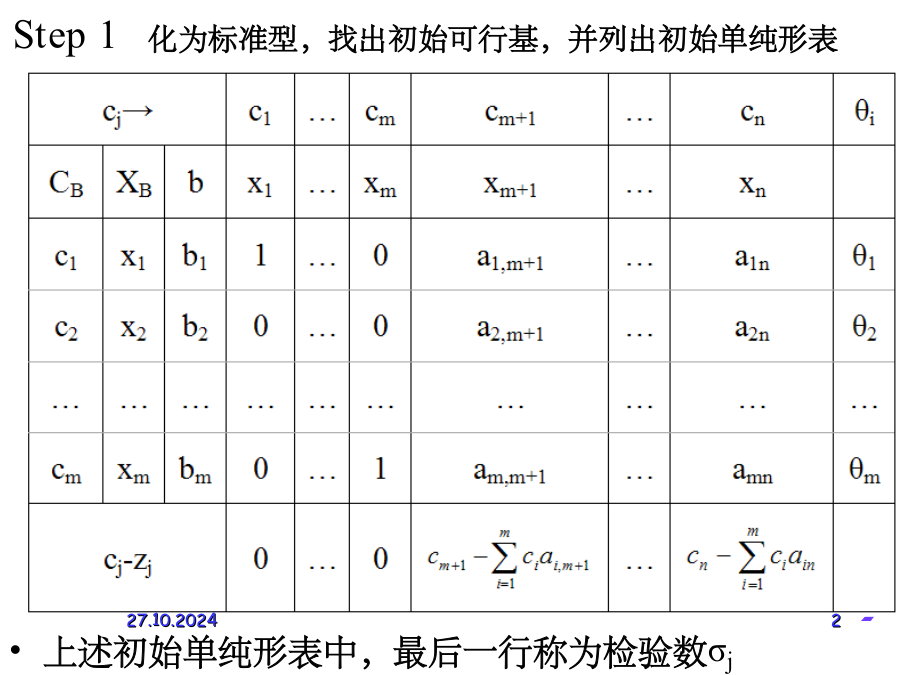
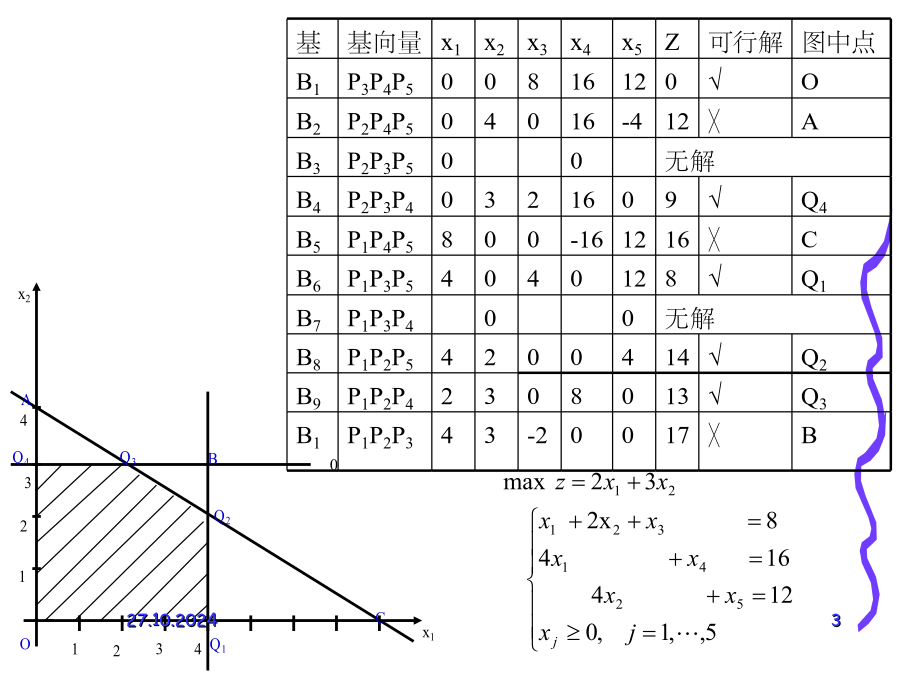
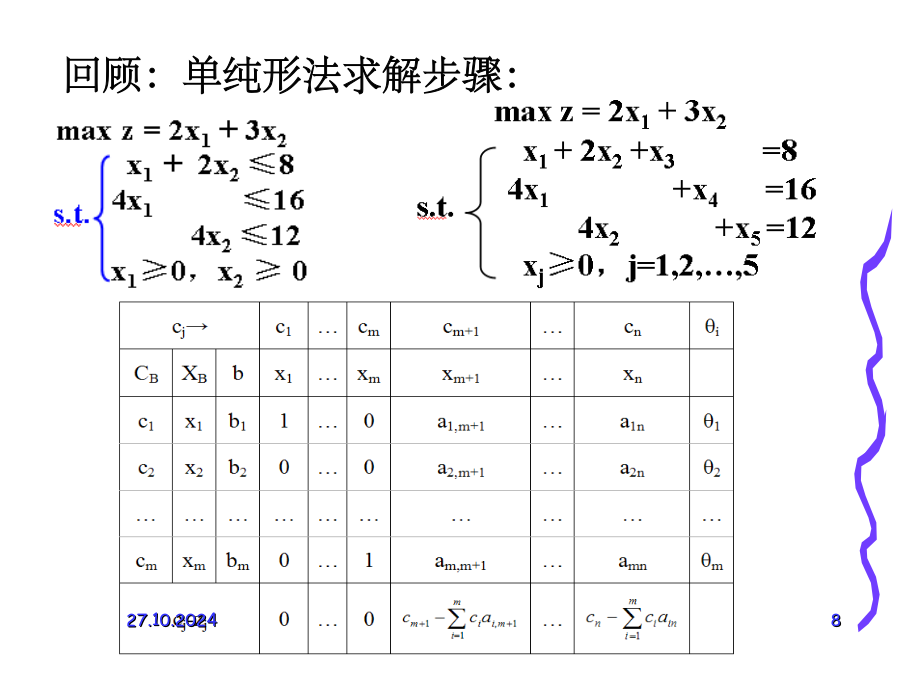
第4节单纯形法计算步骤Step1化为标准型，找出初始可行基，并列出初始单纯形表基Step2：检查非基变量所对应的检验数σj，若所有的σj≤0，则当前的基可行解就是最优解，当前的目标函数值就是最优值，停止计算。
否则，转入下一步。

Step3：若存在一个σk>0，σk所对应的变量xk的系数列向量Pk≤0(即Pk中每一个分量aik≤0)，则该LP无有限最优解，停止计算。
否则，转入下一步。

Step4：进行可行基的迭代。

重复以上步骤
例7用单纯形法求解例6。
maxz=2x1+3x2练习：解：回顾：单纯形法求解步骤：
第5节单纯形法的进一步讨论第5节单纯形法的进一步讨论MaxZ=-3x1+x3
x1+x2+x3≤4
-2x1+x2-x3≥1
3x2+x3=9
xi≥0,j=1,2,3二、两阶段法
第一阶段暂不考虑原问题是否存在基可行解，给原问题加入人工变量，并构建一个仅含人工变量的目标函数（求极小化），人工变量的价值系数一般为1，约束条件和原问题的一样。
当第一阶段中目标函数的最优值＝0，即人工变量＝0，则转入第二阶段；若第一阶段中目标函数的最优值不等于0，即人工变量不等于0，则判断原问题为无解。
第二阶段：将第一阶段计算所得的单纯形表划去人工变量所在的列，并将目标函数换为原问题的目标函数作为第二阶段的初始单纯形表，进行进一步的求解。求解辅助问题，得到辅助问题的最优解（第二阶段）单纯形表2单纯形法小结第5节单纯形法的进一步讨论目标函数极小化时解的最优性判别；
无可行解的判别；
无界的判别；
无穷多最优解的判别；
唯一最优解的判别.例3:复习题：下表为一求解极大值线性规划问题的初始单纯型表及迭代后的表，为松弛变量，试求表中a~L的值及各变量下标m~t的值；第6节应用举例建模步骤：一般的产品计划问题举例例1：数学模型：例2合理下料问题。
现要截取2.9米、2.1米和1.5米的圆钢各100根。而现在仅有一批长7.4米的棒料毛坯，问应如何下料，才能使所消耗的原材料最省。练习1：例4.连续投资问题。P53,2-13

练习：第一章总结基本问题：单纯形法小结添加松弛变量、人工变量列出初始单纯形表对任一
有