
第8讲SPSS的因子分析ppt课件.ppt

lj****88




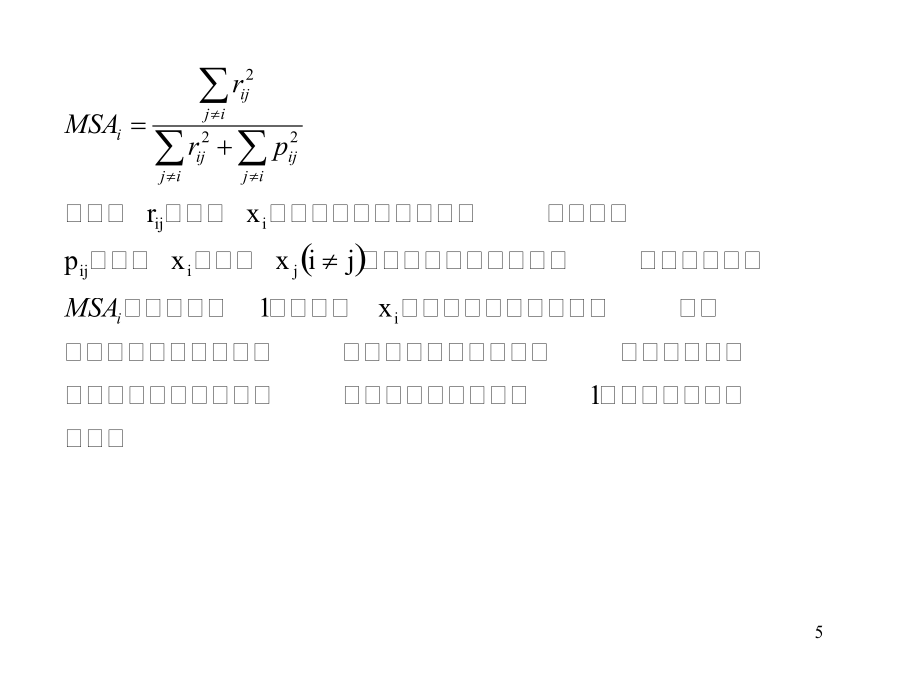




亲,该文档总共29页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

第8讲SPSS的因子分析ppt课件.ppt
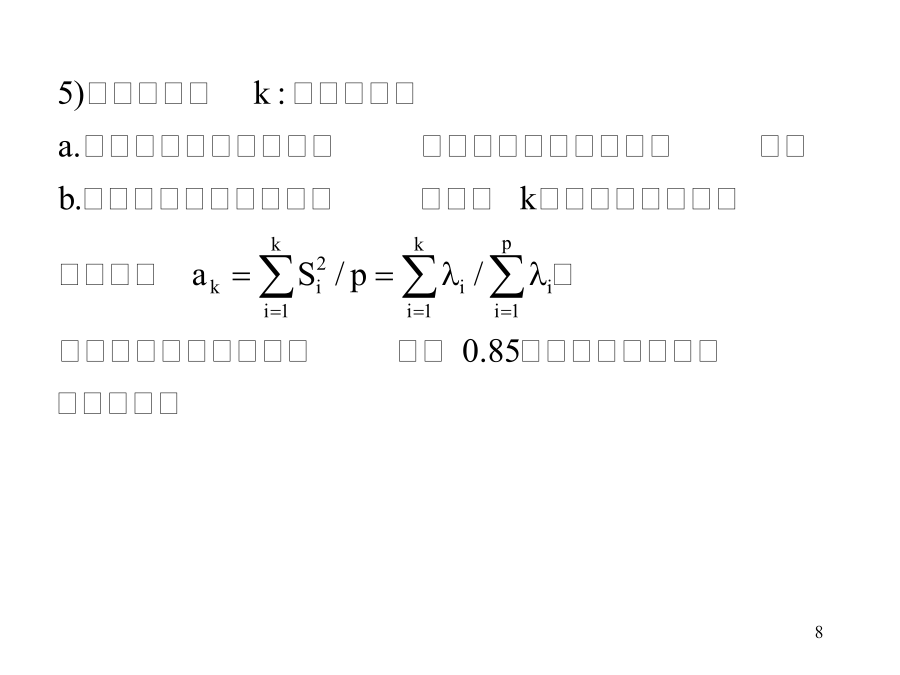
第8讲SPSS的因子分析X1=a11f1+a12f2+…+a1kfk+u1…Xp+ap1f1+ap2f2+…+apkfk+up该模型的矩阵表示为X=AF+u其中,A称为因子载荷矩阵。变量xi的共通度(Communality):hi2=ai12+ai22+…aik2反映全体因子对改变量的解释程度。如果大多数原有变量的共同度均较高(如80%以上),则说明提取的因子能反映原有变量的大部分信息。因子fi的方差贡献:Sj2=a1j2+a2j2+…apj2反映该因子对原有变量总方差的解释能力,是衡量因子重要性的指标。

第讲SPSS的因子分析PPT课件.ppt
12345678910111213142024/11/316171819202122232425262728292024/11/3

spss 第8讲 因子分析与对应分析.ppt
8.1因子分析R型因子分析因子分析的几个概念1、因子载荷2、变量共同度3、公因子Fj的方差贡献4、因子旋转因子旋转的目的是为了使得因子载荷阵的结构简化,便于对公共因子进行解释。这里所谓的结构简化是使每个变量仅在一个公共因子上有较大的载荷,而在其余公共因子上载荷比较小。这种变换因子载荷阵的方法称为因子轴的旋转。旋转的方法有很多种,如正交旋转,斜交旋轴等。5、因子得分因子分析的一般步骤利用因子分析过程分析各个城市的市政设施建设情况执行【Analyze】/【DimensionReduction】/【Factor

第8章-因子分析与聚类分析(含SPSS)(ppt文档).ppt
第八章因子分析与聚类分析本章内容第一节因子分析(二)因子分析的特点1、因子变量的数量远少于原有指标变量的数量。2、因子变量并不是原有变量的简单取舍,而是对原有变量的重新组构。3、因子之间线性关系不显著。4、因子变量具有命名解释性。二、因子分析的数学模型和相关概念(一)因子分析的数学模型因子分析的数学模型为:(8.1)写成矩阵形式为,其中为原始变量向量,为公因子载荷矩阵,为公共因子,为特殊因子。(二)因子分析中的基本概念1、因子的含义因子分析法中提到两种因子:公共因子和特殊因子。公共因子是每个原有变量的线性

第8章-因子分析与聚类分析(含SPSS)(ppt文档).ppt
第八章因子分析与聚类分析本章内容第一节因子分析(二)因子分析的特点1、因子变量的数量远少于原有指标变量的数量。2、因子变量并不是原有变量的简单取舍,而是对原有变量的重新组构。3、因子之间线性关系不显著。4、因子变量具有命名解释性。二、因子分析的数学模型和相关概念(一)因子分析的数学模型因子分析的数学模型为:(8.1)写成矩阵形式为,其中为原始变量向量,为公因子载荷矩阵,为公共因子,为特殊因子。(二)因子分析中的基本概念1、因子的含义因子分析法中提到两种因子:公共因子和特殊因子。公共因子是每个原有变量的线性
