循环码BCH码卷积码ppt课件.ppt

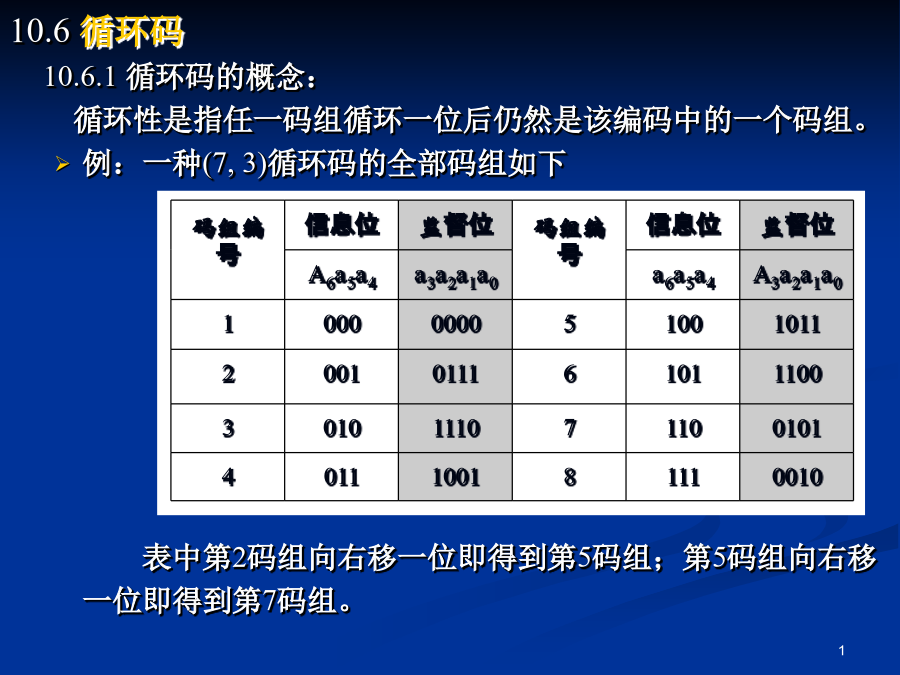
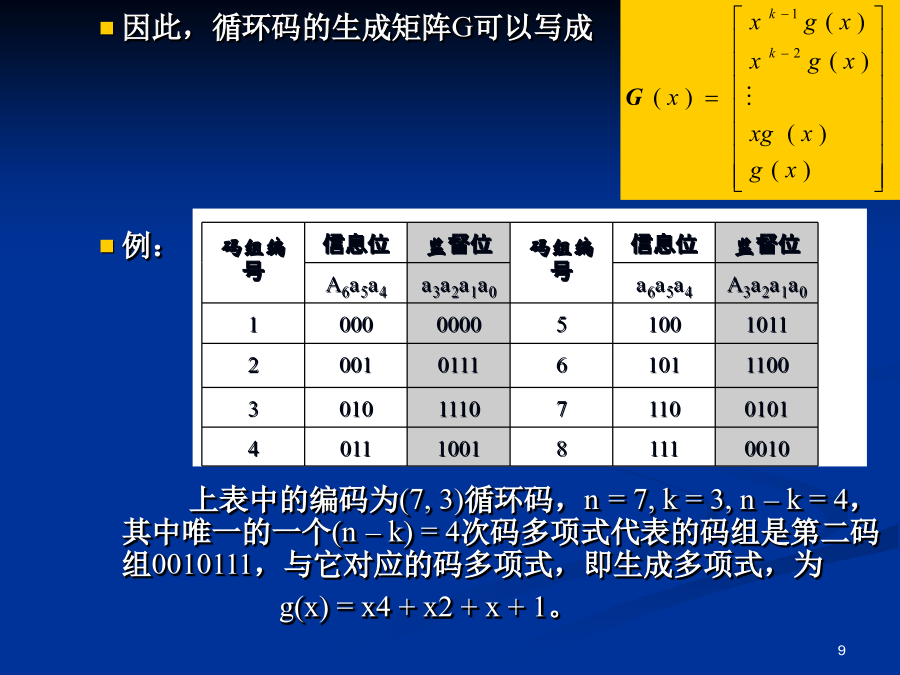
10.6循环码
10.6.1循环码的概念：
循环性是指任一码组循环一位后仍然是该编码中的一个码组。
例：一种(7,3)循环码的全部码组如下

表中第2码组向右移一位即得到第5码组；第5码组向右移一位即得到第7码组。一般情况
若(an-1an-2…a0)是循环码的一个码组，则循环移位后的码组： (an-2an-3…a0an-1)
(an-3an-4…an-1an-2)
…… (a0an-1…a2a1)
仍然是该编码中的码组。
多项式表示法
一个长度为n的码组(an-1an-2…a0)可以表示成

上式中x的值没有任何意义，仅用它的幂代表码元的位置。
例：码组1100101可以表示为10.6.2循环码的运算
整数的按模运算
在整数运算中，有模n运算。例如，在模2运算中，有
1+1=20(模2)， 1+2=31(模2)，23=60(模2)
等等。
一般说来，若一个整数m可以表示为

式中，Q为整数，则在模n运算下，有
mp(模n)
所以，在模n运算下，一个整数m等于它被n除得的余数。码多项式的按模运算
若任意一个多项式F(x)被一个n次多项式N(x)除，得到商式Q(x)和一个次数小于n的余式R(x)，即

则在按模N(x)运算下，有

这时，码多项式系数仍按模2运算。
例1：x3被(x3+1)除，得到余项1，即
例2：
因为
x
x3+1x4+x2+1
x4+x
x2+x+1
在模2运算中加法和减法一样。循环码的数学表示法
在循环码中，设T(x)是一个长度为n的码组，若

则T(x)也是该编码中的一个码组。
上式中的T(x)正是码组T(x)向左循环移位i次的结果。
例：一循环码为1100101，即
若给定i=3，则有

上式对应的码组为0101110，它正是T(x)向左移3位的结果。
结论：一个长为n的循环码必定为按模(xn+1)运算的一个余式。循环码的生成
有了生成矩阵G，就可以由k个信息位得出整个码组：
例：
式中，

生成矩阵G的每一行都是一个码组。
因此，若能找到k个已知的码组，就能构成矩阵G。如前所述，这k个已知码组必须是线性不相关的。
在循环码中，一个(n,k)码有2k个不同的码组。若用g(x)表示其中前(k-1)位皆为“0”的码组，则g(x)，xg(x)，x2g(x)，，xk-1g(x)都是码组，而且这k个码组是线性无关的。因此它们可以用来构成此循环码的生成矩阵G。在循环码中除全“0”码组外，再没有连续k位均为“0”的码组。否则，在经过若干次循环移位后将得到k位信息位全为“0”，但监督位不全为“0”的一个码组。这在线性码中显然是不可能的。
因此，g(x)必须是一个常数项不为“0”的(n-k)次多项式，而且这个g(x)还是这种(n,k)码中次数为(n–k)的唯一一个多项式。因为如果有两个，则由码的封闭性，把这两个相加也应该是一个码组，且此码组多项式的次数将小于(n–k)，即连续“0”的个数多于(k–1)。显然，这是与前面的结论矛盾的。
我们称这唯一的(n–k)次多项式g(x)为码的生成多项式。一旦确定了g(x)，则整个(n,k)循环码就被确定了。因此，循环码的生成矩阵G可以写成

例：

上表中的编码为(7,3)循环码，n=7,k=3,n–k=4，其中唯一的一个(n–k)=4次码多项式代表的码组是第二码组0010111，与它对应的码多项式，即生成多项式，为
g(x)=x4+x2+x+1。 g(x)=x4+x2+x+1即“10111”
将此g(x)代入上矩阵，得到

或

上式不符合G=[IkQ]形式，所以它不是典型生成矩阵。但它经过线性变换后，不难化成典型阵。
此循环码组的多项式表示式T(x)：

上式表明，所有码多项式T(x)都能够被g(x)整除，而且任意一个次数不大于(k–1)的多项式乘g(x)都是码多项式。寻求码生成多项式
因为任意一个循环码T(x)都是g(x)的倍式，故它可以写成
T(x)=h(x)g(x)
而生成多项式g(x)本身也是一个码组，即有
T(x)=g(x)
由于码组T(x)是一个(n–k)次多项式，故xkT(x)是一个n次多项式。由

可知，xkT(x)在模(xn+1)运算下也是一个码组，所以有

上式左端分子和分母都是n次多项式，故相除的商式Q(x)=1。因此，上式可以写成将T(x)=h(x)g(x)和T(x)=g(x)代入

化简后，得到

上式表明，生成多项式g(x)应该是(xn+1)的