
关于椭圆形封头的应力分析.docx

快乐****蜜蜂


在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

关于椭圆形封头的应力分析.docx
关于椭圆形封头的应力分析椭圆形封头被广泛应用于许多行业中,如化工、石油、制药等。它们的主要作用是用于储存压缩气体和液体,并在一定范围内缓冲温度和压力的变化。在使用椭圆形封头的过程中,应力分析是必要的,以确保其安全运行。本文将重点介绍椭圆形封头的应力分析。椭圆形封头由于其形状的不规则性,其应力分析相对于圆形封头来说更为复杂。为了简化问题,我们将使用椭圆形封头的长轴作为坐标轴,这样,椭圆形封头的横截面可以看作是一个半径为R1,长度为2R2的椭圆。椭圆形封头的应力分析主要涉及到内压和热载荷对其造成的应力。对于内

多接管标准椭圆形封头应力分析与安全评定.docx
多接管标准椭圆形封头应力分析与安全评定标准椭圆形封头作为常见的容器件在工程中广泛应用。在实际应用中,为了满足容器的设计要求,常会通过多接管方式对椭圆形封头进行加工改造。在多接管标准椭圆形封头的设计和使用过程中,需要进行应力分析和安全评定,以确保容器在使用过程中的稳定性和安全性。本文将结合实际案例,介绍多接管标准椭圆形封头的应力分析和安全评定方法。一、标准椭圆形封头的结构特点及应用标准椭圆形封头是一种球冠形封头的变形。其外形呈扁平椭圆形,轴线与短轴之比一般为2:1。标准椭圆形封头的结构特点是外形简单,制造工

椭圆形封头开孔孔边应力集中分析.docx
椭圆形封头开孔孔边应力集中分析椭圆形封头开孔孔边应力集中分析椭圆形封头作为一种传统的压力容器封头形式,在工业生产中应用广泛。而在实际应用中,封头表面经常需要开一个孔洞进行物料进出口控制。在孔洞开辟过程中,会导致封头的局部应力集中问题,进而对封头的使用寿命、安全性以及操作效率产生影响。因此,对椭圆形封头开孔孔边应力集中的分析与研究是很有必要的。一、椭圆形封头开孔孔边应力集中的原因椭圆形封头开孔孔边应力集中主要是由于孔洞开辟过程中非均匀应力状态的形成。其中,孔洞周围的材料断裂可视为应力集中,特别在孔边角部分,

椭圆形封头的尺寸.doc
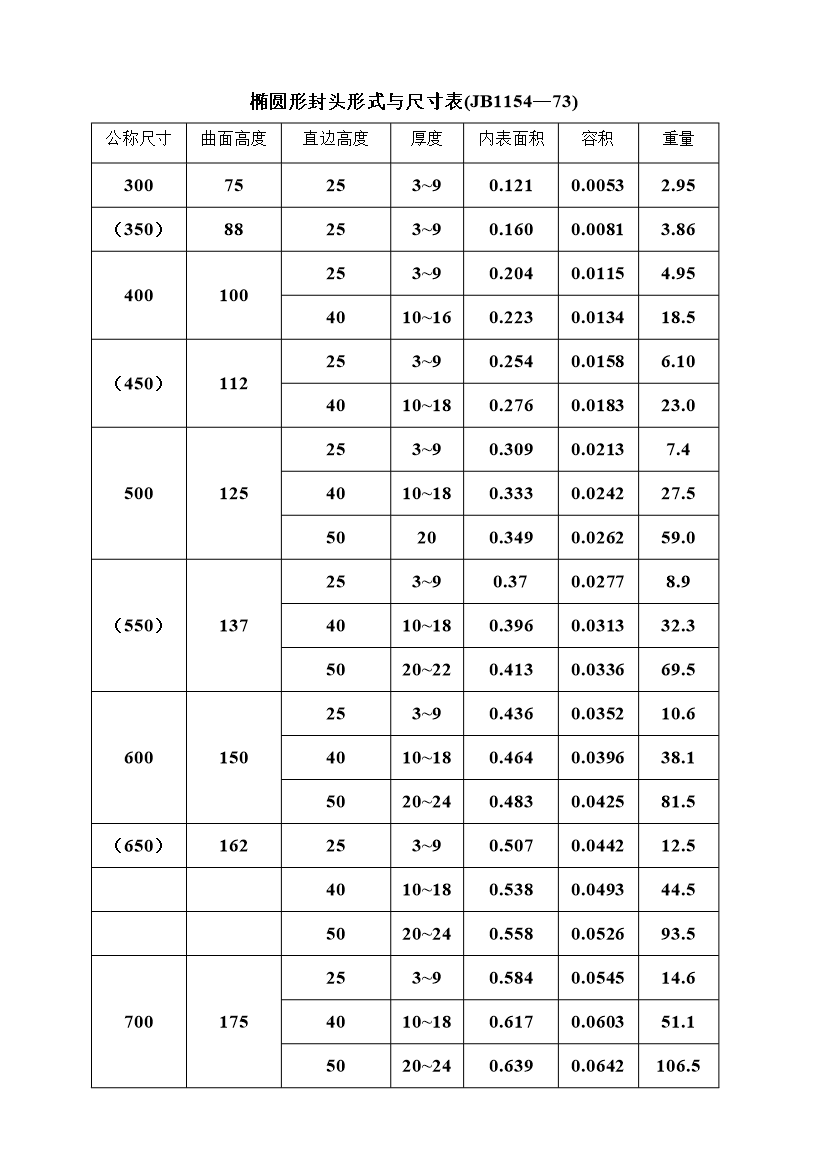
椭圆形封头形式与尺寸表(JB1154—73)公称尺寸曲面高度直边高度厚度内表面积容积重量30075253~90.1210.00532.95(350)88253~90.1600.00813.86400100253~90.2040.01154.954010~160.2230.013418.5(450)112253~90.2540.01586.104010~180.2760.018323.0500125253~90.3090.02137.44010~180.3330.024227.550200.3490.026
椭圆形封头的尺寸.doc
椭圆形封头形式与尺寸表(JB1154—73)公称尺寸曲面高度直边高度厚度内表面积容积重量30075253~90.1210.00532.95(350)88253~90.1600.00813.86400100253~90.2040.01154.954010~160.2230.013418.5(450)112253~90.2540.01586.104010~180.2760.018323.0500125253~90.3090.02137.44010~180.3330.024227.550200.3490.026
