BP神经网络的改进和MATLAB实现ppt课件.ppt

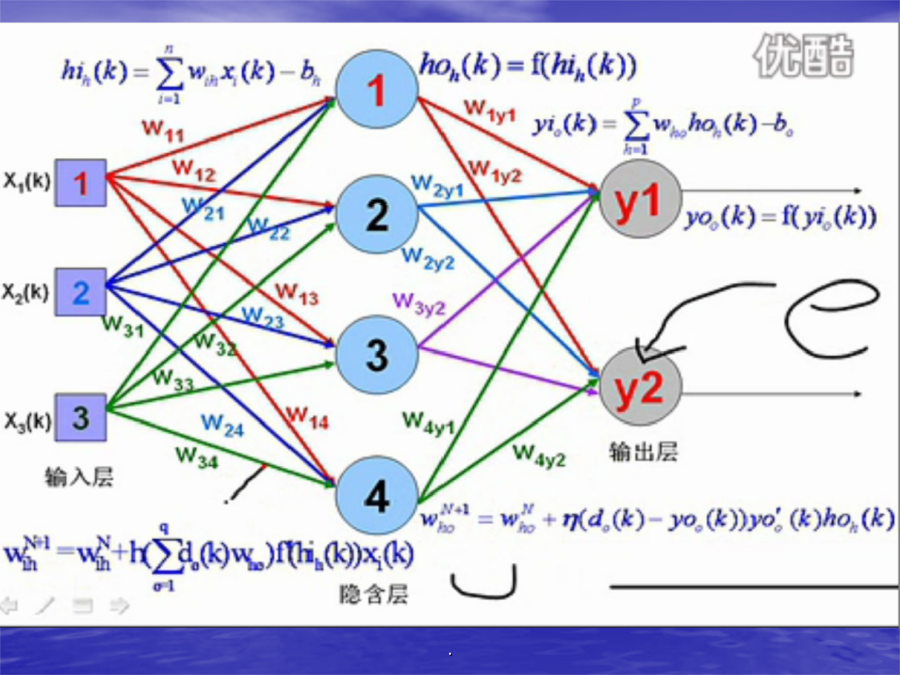
改进BP神经网络与MATLAB实现

江西师范大学

2012.6.111：BP神经网络的概述
2：BP神经网络的标准训练学习
3：在MATLAB软件上运行几个程序
4：基于Levenberg-Marquardt算法的学习优 化（阻尼最小二乘法）
5：基于蚁群算法的初始权值优化
6：经过4和5优化后的仿真试验（发动机 性能趋势分析和故障诊断中的应用）
7：总结多元函数图示多元函数图示多元函数及其图形.BP神经网络模型BP神经网络模型.网络结构
输入层有n个神经元，隐含层有p个神经元,
输出层有q个神经元
变量定义
输入向量;
隐含层输入向量；
隐含层输出向量;
输出层输入向量;
输出层输出向量;
期望输出向量;
输入层与中间层的连接权值:
隐含层与输出层的连接权值:
隐含层各神经元的阈值:
输出层各神经元的阈值:
样本数据个数:
激活函数:
误差函数：
第一步，网络初始化
给各连接权值分别赋一个区间（-1，1）内的随机数，设定误差函数e，给定计算精度值和最大学习次数M。
第二步,随机选取第个输入样本及对应期望输出第三步，计算隐含层各神经元的输入和输出
第四步，利用网络期望输出和实际输出，计算误差函数对输出层的各神经元的偏导数 。第五步，利用隐含层到输出层的连接权值、输出层的 和隐含层的输出计算误差函数对隐含层各神经元的偏导数 .第六步，利用输出层各神经元的 和隐含层各神经元的输出来修正连接权值第七步，利用隐含层各神经元的和输入层各神经元的输入修正连接权。第八步，计算全局误差

第九步，判断网络误差是否满足要求。当误差达到预设精度或学习次数大于设定的最大次数，则结束算法。否则，选取下一个学习样本及对应的期望输出，返回到第三步，进入下一轮学习。
BP算法直观解释
情况1的直观表达
当误差对权值的偏
导数大于零时，权值
调整量为负，实际输
出大于期望输出，
权值向减少方向调整，
使得实际输出与期望
输出的差减少。BP算法直解释
情况2的直观表达
当误差对权值的偏导数
小于零时，权值调整量
为正，实际输出少于期
望输出，权值向增大方向
调整，使得实际输出与期
望输出的差减少。

梯度下降法一、无约束优化的古典分析法
无约束优化问题可表示为
minf(x1,x2,…,xn)
xiR，i=1,2,…,n
如果令x=(x1,x2,…,xn)T，则无约束优化问题为
minf(x)
xRn关于f(x)：
当x=(x)时，f(x)是一条曲线；
当x=(x1,x2)T时，f(x1,x2)是一个曲面；
当x=(x1,x2,x3)T时，f(x1,x2,x3)是一个体密度(或类位势函数)；
当x=(x1,x2,…,xn)T时，f(x1,x2,…,xn)是一个超曲面。设函数f(x)=f(x1,...,xn)对所有变元都有一阶与二阶连续偏导数，则
①称n个一阶偏导数构成的n维列向量为f.(x)的梯度，记作

②称满足f(x0)=0的点x0为函数f(x)的驻点或临界点。③称n2个二阶偏导数构成的n阶对称矩阵为函数f(x)的海森(Hessian)矩阵，记为H(x)或2f(x)：综上所述，多元函数f(x)=f(x1,x2,…,xn)的一阶导数是它的梯度f.(x)，二阶导数是它的Hessian矩阵2f(x)。
在最优化方法的讨论中这是两个常用的概念。定理(最优性条件)设n元函数y=f(x)对所有变元具有一阶及二阶连续偏导数，则x0是f(x)极小点的充分条件为
f(x0)=0，2f(x0)>0(正定)
而x0是f(x)极大点的充分条件为
f(x0)=0，2f(x0)<0(负定)
事实上，如果设x=(x1,…,xn)T，则利用多元函数的泰勒展开式，我们有其中R为x的高阶无穷小，即R=o||x||2。
于是，当x0为函数f.(x)的驻点时可以得到

于是，当xi(i=1,…,n)足够小时，上式右端的正负号完全由二次型xT2f(x0)x决定，从而完全由Hessian矩阵2f(x)的正(负)定性决定。
注记：微积分中求一元函数和二元函数极值的方法，是这个定理的特例。二、无约束优化的梯度下降法
对于无约束优化问题
minf(x)(1)
x=(x1,x2,…,xn)TRn
如果f(x)可微，根据古典分析的方法，可利用
f(x)=0(2)
求驻点，然后再利用Hessian矩阵2f.(x)来判定这些驻点是否极小值点，从而求出无约束优化问题(1)的最优解。但是，用古典分析的方法求解无约束优化问题(1)实际上是行不通的，这是由于：
(1)实际应用中相当数量的函数f.(x)不具有解析性，故非线性方程组f(x)=0无法形成；
(2)即使形成了方程组f(x)=0，由于它是一个n元非线性方程组，因而求它的解与解决原问题一样地