混凝土单轴应力应变关系.pdf

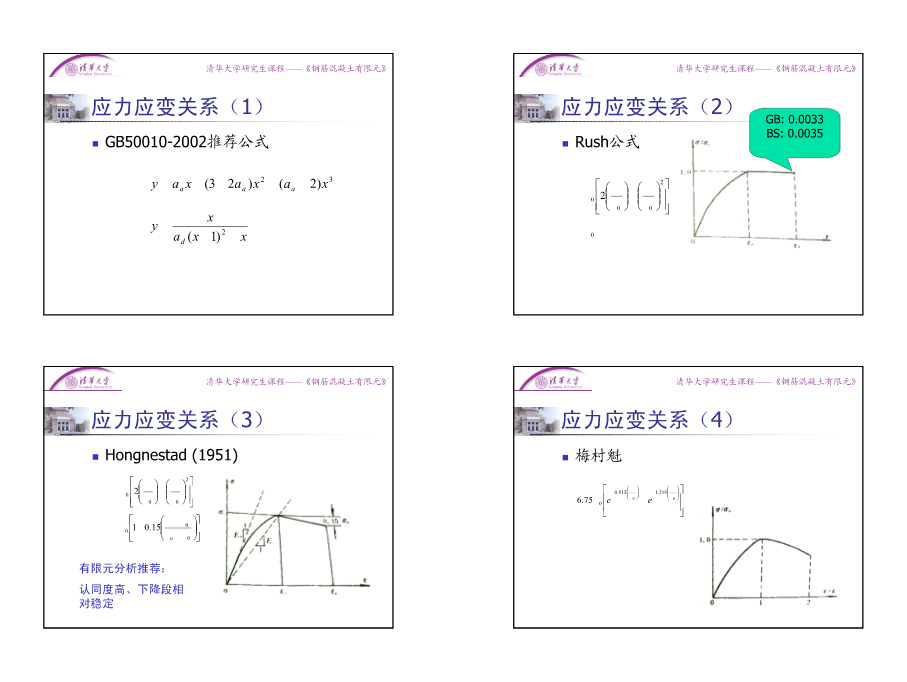
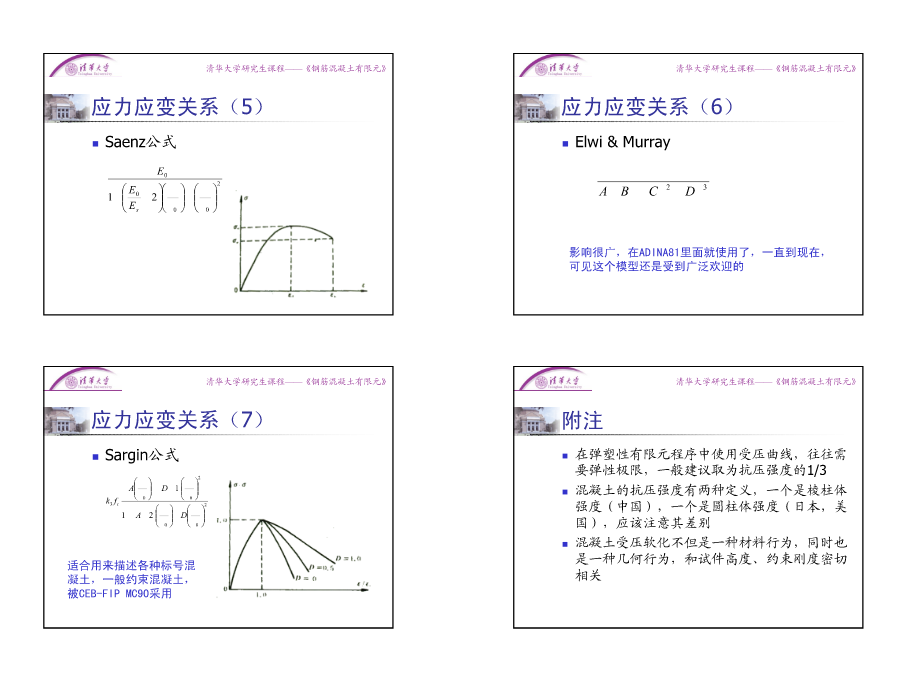
清华大学研究——《钢筋混凝土有生课程限元》清华大学研究——《钢筋混凝土有生课程限元》

混凝土的组成

„混凝土：

混凝土的单轴应力应变关系„微观层次：水泥凝胶、氢氧化钙结晶、未
水化的水泥颗粒、空隙、毛细管、孔隙水、
气泡……

„细观层次：水泥浆、粗骨料
江见鲸陆新征
„宏观层次：均匀材料
清华大学土木系区分界限：
2004小于骨料粒径、骨料粒径、3倍骨料粒径

清华大学研究——《钢筋混凝土有生课程限元》清华大学研究——《钢筋混凝土有生课程限元》

应力应变关系典型单轴应力应变关系

„骨料与砂浆之间的交界面是混凝土的薄„0～a，弹性阶段

弱环节„a~b，裂缝稳定扩展阶段

„c~d，不稳定裂纹扩展阶段

1
清华大学研究生课程——《钢筋混凝土有限元》清华大学研究生课程——《钢筋混凝土有限元》

体积膨胀不同标号混凝土

„应力

„应变
混凝土

加载头刚性构件

清华大学研究生课程——《钢筋混凝土有限元》清华大学研究生课程——《钢筋混凝土有限元》

加载速度侧向约束

„非常高的速度加载(核爆炸)，可以提高混„支座、箍筋、侧压力……
凝土强度20％～30％

2
清华大学研究生课程——《钢筋混凝土有限元》清华大学研究生课程——《钢筋混凝土有限元》

应力应变关系（1）应力应变关系（2）
GB:0.0033
BS:0.0035
„GB50010-2002推荐公式„Rush公式

=+−2+−32
yaax(32aa)x(aa2)xεε
σ=σ2−
0εε
00
x
y=σ=σ
−2+0
ad(x1)x

清华大学研究生课程——《钢筋混凝土有限元》清华大学研究生课程——《钢筋混凝土有限元》

应力应变关系（3）应力应变关系（4）

„Hongnestad(1951)„梅村魁

εε2
εε
σ=σ−−0.812−1.218
02εε
εε00
00σ=6.75σe−e
0

ε−ε
σ=σ1−0.150
0ε−ε
u0

有限元分析推荐：
认同度高、下降段相
对稳定

3
清华大学研究生课程——《钢筋混凝土有限元》清华大学研究生课程——《钢筋混凝土有限元》

应力应变关系（5）应力应变关系（6）

„Saenz公式„Elwi&Murray

Eεε
σ=0
2σ=
Eεε+ε+ε2+ε3
1+0−2+ABCD
εε
Es00

影响很广，在ADINA81里面就使用了，一直到现在，
可见这个模型还是受到广泛欢迎的

清华大学研究生课程——《钢筋混凝土有限元》清华大学研究生课程——《钢筋混凝土有限元》

应力应变关系（7）附注

„Sargin公式„在弹塑性有限元程序中使用受压曲线，往往需
要弹性极限，一般建议取为抗压强度的1/3
2
εε
A+()D−1
εε„混凝土的抗压强度有两种定义，一个是棱柱体
σ=00
k3fc2
εε强度（中国），一个是圆柱体强度（日本，美
1+()A−2+D
εε
00国），应该注意其差别

„混凝土受压软化不但是一种材料行为，同时也
适合用来描述各种标号混是一种几何行为，和试件高度、约束刚度密切
凝土，一般约束混凝土，相关
被CEB-FIPMC90采用

4
清华大学研究生课程——《钢筋混凝土有限元》清华大学研究生课程——《钢筋混凝土有限元》

混凝土受拉应力应变关系混凝土受拉曲线的表示方法

„早期对混凝土的认识：脆性材料、受拉不存在„基于裂缝宽度的表示方法
下降段
„优点：与标距无关，与构件尺寸关系不大
„精细试验发现混凝土受拉也存在一个下降段
„缺点：裂缝宽度观测非常困难，而且是构件
„现在一般认为混凝土、岩石等属于半脆性材料表面裂缝的宽度
（quasi-brittle）
„基于应变的表示方法
„混凝土受拉更容易受到偶然因素的影响，比受
„优点：量测容易
压更加不稳定
„缺点：受标距、构件尺寸影响较大

清华大学研究生课程——《钢筋混凝土有限元》清华大学研究生课程——《钢筋混凝土有限元》

常用软化曲线表示方法举例

„直线下降型

„双折线下降型

„指数下降型

„幂函数下降型

„分数下降型

5
清华大学研究生课程——《钢筋混凝土有限元》

作业

„任选三种受压应力应变关系

σε
„作曲线
fε
c0

„求Es,Et

6