动态问题中的最值问题-豆柴文库

动态问题中的最值问题.ppt

2024-10-24

16金币

331KB

14页

xf****65

实名认证

内容提供者

1/10

2/10

3/10

4/10

5/10

6/10

7/10

8/10

9/10

10/10

亲，该文档总共14页，到这已经超出免费预览范围，如果喜欢就直接下载吧～

下载提示文本预览

如果您无法下载资料，请参考说明：

1、部分资料下载需要金币，请确保您的账户上有足够的金币

2、已购买过的文档，再次下载不重复扣费

3、资料包下载后请先用软件解压，在使用对应软件打开

相关资料

动态问题中的最值问题.ppt

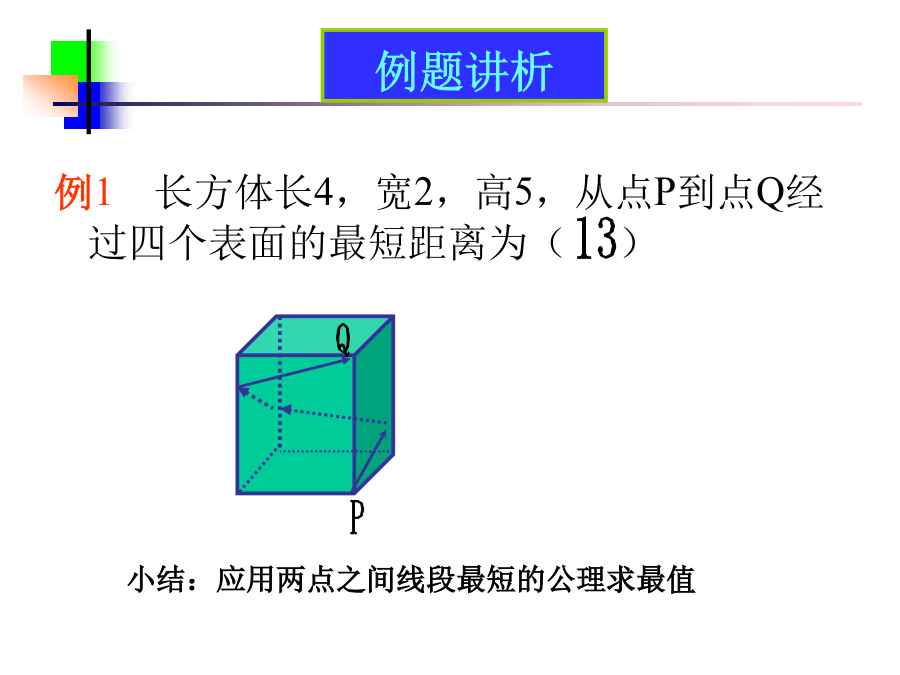
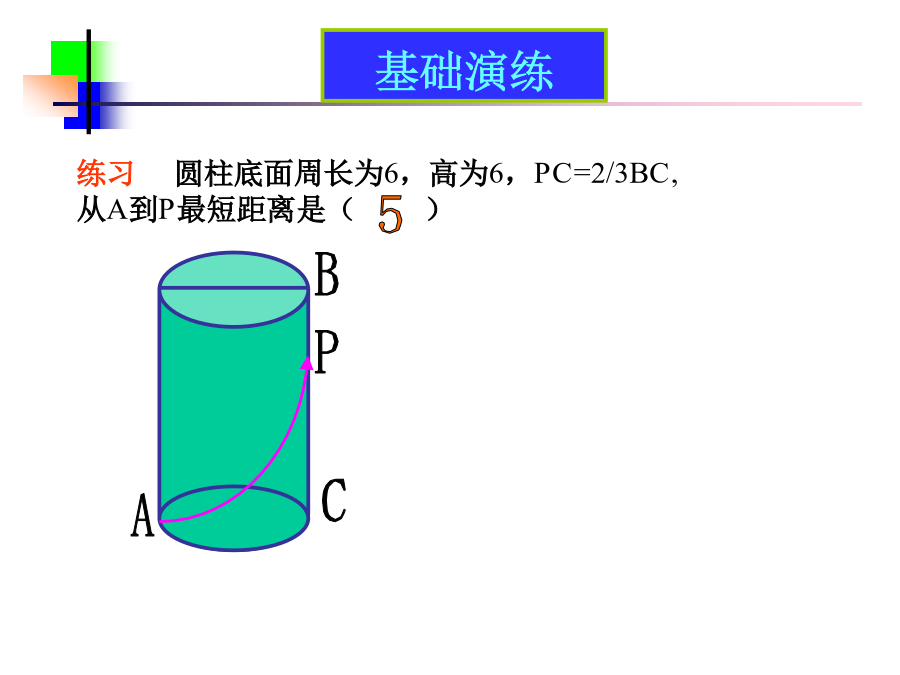
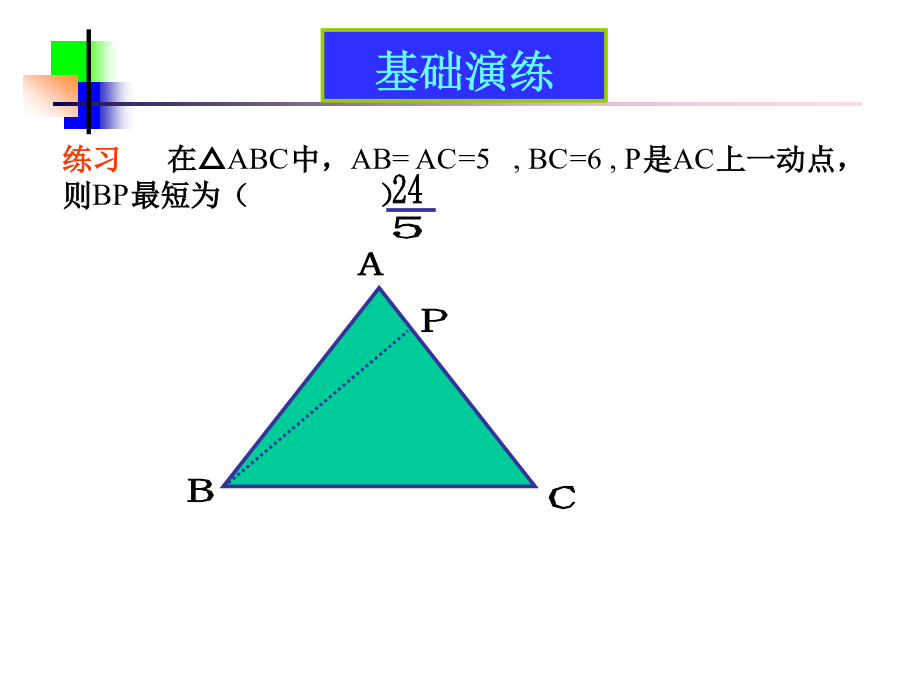
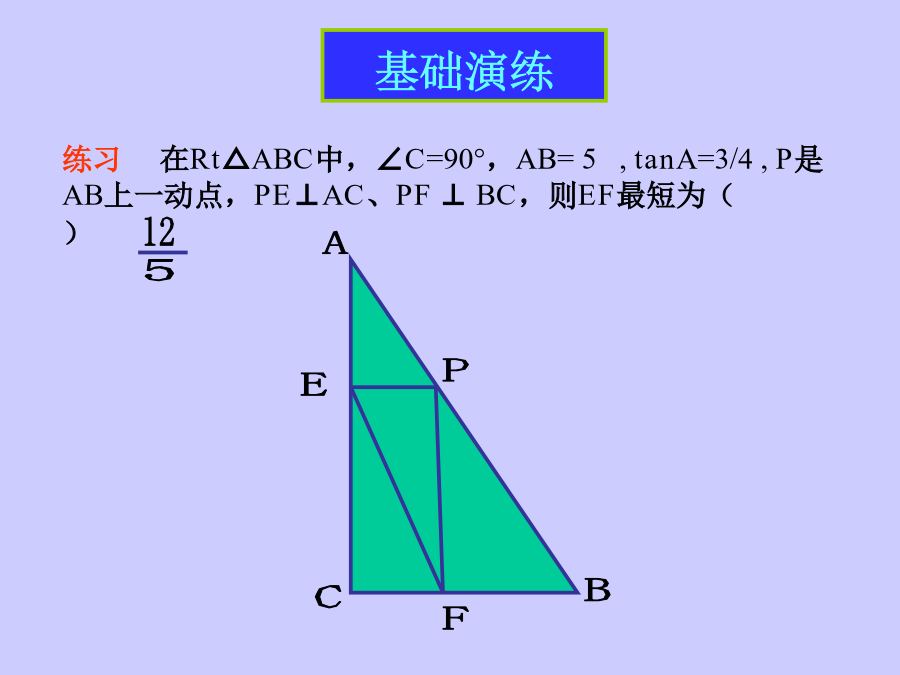
动态问题中的最值问题（1）1.应用两点之间线段最短的公理求最值2.应用垂线段最短的性质求最值3.应用点到圆的距离求最值4.应用轴对称的性质求最值5.应用其它知识求最值例1长方体长4，宽2，高5，从点P到点Q经过四个表面的最短距离为（）基础演练例2四边形ABCD中，∠A=90°，AD=4，BD平分∠ABC，点P是BC上的动点，则PD最短距离为（）基础演练基础演练基础演练课堂小结：1.应用两点之间线段最短的公理求最值2.应用垂线段最短的性质求最值3.应用点到圆的距离求最值提升演练练习2△ABC中，∠C=45°

2024-10-24

331KB

动态最值问题.doc

\\\初三数学讲义专题复习——动态几何之最值问题一．课堂衔接1.课前交流，帮助整理知识点。2.复习旧知，课前练习。动态题是近年来中考的的一个热点问题，动态包括点动、线动和面动三大类，解这类题目要“以静制动”，即把动态问题，变为静态问题来解，而静态问题又是动态问题的特殊情况。常见的题型包括最值问题、面积问题、和差问题、定值问题和存在性问题等。在平面几何的动态问题中，当某几何元素在给定条件变动时，求某几何量（如线段的长度、图形的周长或面积、角的度数以及它们的和与差）的最大值或最小值问题，称为最

2024-08-17

262KB

应用题中的最值问题.doc

“华杯赛”专题讲座第页应用题中的最值问题例1.某银行定期储蓄的种类和利率如下表所示，假如你有1000元钱，想存四年，那么你最多可以得到多少元利息？存款时间（年）年利率到期利率10.030.0320.03750.07530.04250.1275分析：如果将s元本金先存一个n年期，到期利率是a，再存一个m年期，到期利率是b，那么最终获得金额为元。[答疑编号505721560101]【答案】161.325【解答】由于最终获得的利息与存款的顺序没有关系，所以存4年共有以下几种方案：①四个1年期；②两个1年期和一个

2024-10-27

91KB

动态问题---最值1.docx

动态问题---最值教学目标：1.经历探索解决线段的最值问题的过程，学会将问题转化为线段的最值。2.培养学生转化思想，提高合情推理能力。重点难点：重点难点是抽象出数学模型教学过程：一、例题分析例1.（2014•宿迁）如图，正方形ABCD的边长为2，点E为边BC的中点，点P在对角线BD上移动，则PE+PC的最小值是．变式1：菱形ABCD中，∠A＝60°，AB＝3，P是边CD的动点，则PA＋PB的最小值是变式2.如图，抛物线与坐标轴分别交于A（-3，0）、B（1,0）、C（0,3），顶点D（-1，4）（1）P是

动态问题---最值1.docx