
季节性时间序列分析方法.docx

羽沫****魔王










亲,该文档总共43页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料
季节性时间序列分析方法.docx
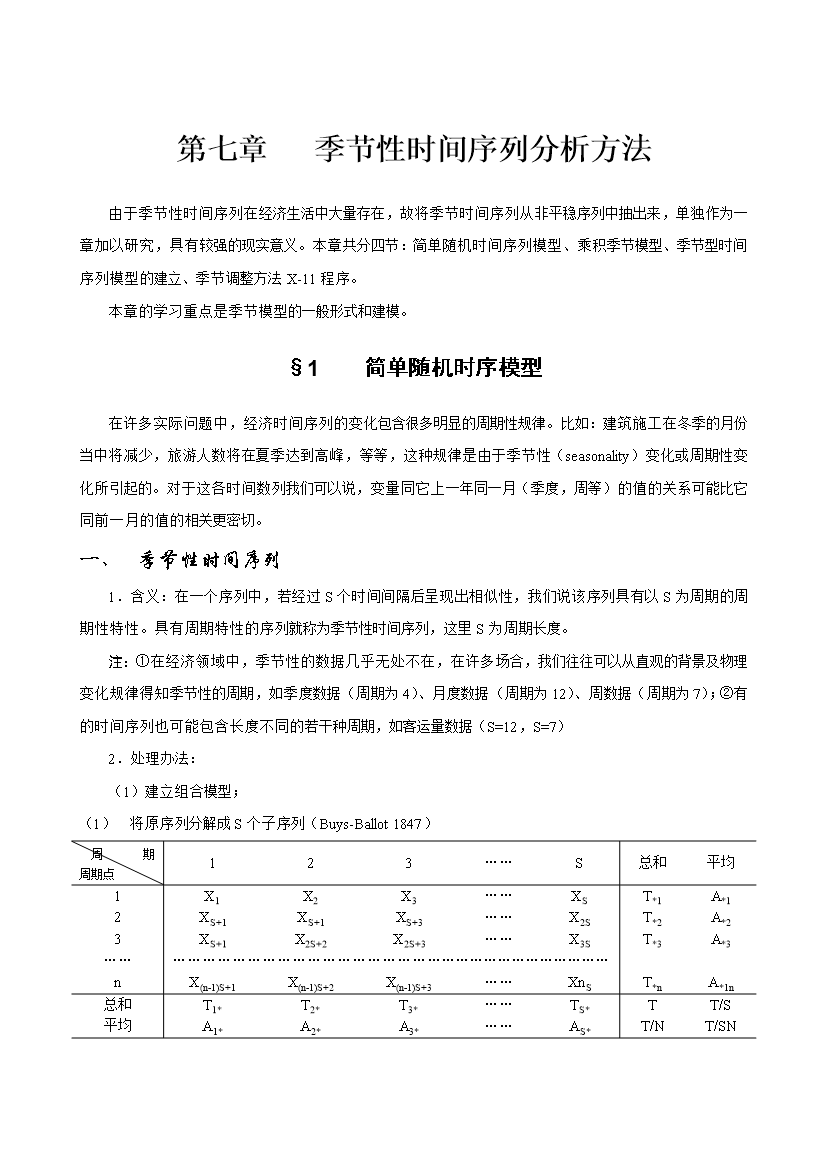
第七章季节性时间序列分析方法由于季节性时间序列在经济生活中大量存在故将季节时间序列从非平稳序列中抽出来单独作为一章加以研究具有较强的现实意义。本章共分四节:简单随机时间序列模型、乘积季节模型、季节型时间序列模型的建立、季节调整方法X-11程序。本章的学习重点是季节模型的一般形式和建模。§1简单随机时序模型在许多实际问题中经济时间序列的变化包含很多明显的周期性规律。比如:建筑施工在冬季的月份当中将减少旅游人数将在夏季达到高峰等等这种规律是由于季节性(seasonality)变化或周期性变化所引

季节性时间序列分析方法.docx
第七章季节性时间序列分析方法由于季节性时间序列在经济生活中大量存在,故将季节时间序列从非平稳序列中抽出来,单独作为一章加以研究,具有较强的现实意义。本章共分四节:简单随机时间序列模型、乘积季节模型、季节型时间序列模型的建立、季节调整方法X-11程序。本章的学习重点是季节模型的一般形式和建模。§1简单随机时序模型在许多实际问题中,经济时间序列的变化包含很多明显的周期性规律。比如:建筑施工在冬季的月份当中将减少,旅游人数将在夏季达到高峰,等等,这种规律是由于季节性(seasonality)变化或周期性变化所引

季节性时间序列分析方法.docx
第七章季节性时间序列分析方法由于季节性时间序列在经济生活中大量存在,故将季节时间序列从非平稳序列中抽出来,单独作为一章加以研究,具有较强的现实意义。本章共分四节:简单随机时间序列模型、乘积季节模型、季节型时间序列模型的建立、季节调整方法X-11程序。本章的学习重点是季节模型的一般形式和建模。§1简单随机时序模型在许多实际问题中,经济时间序列的变化包含很多明显的周期性规律。比如:建筑施工在冬季的月份当中将减少,旅游人数将在夏季达到高峰,等等,这种规律是由于季节性(seasonality)变化或周期性变化所引

季节性时间序列分析方法.ppt
第七章季节性时间序列分析方法

季节性时间序列分析方法ppt课件.ppt
第七章季节性时间序列分析方法2345678910111213141516171819202122232425262728293031323334353637
