
波动方程ppt课件.ppt

ca****ng






亲,该文档总共49页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

波动方程ppt课件.ppt
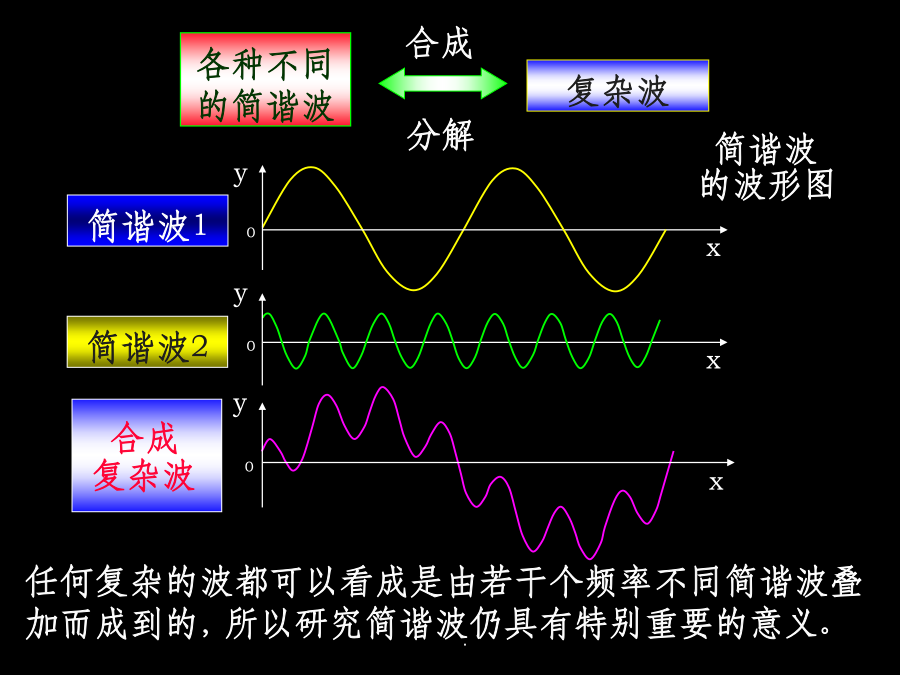
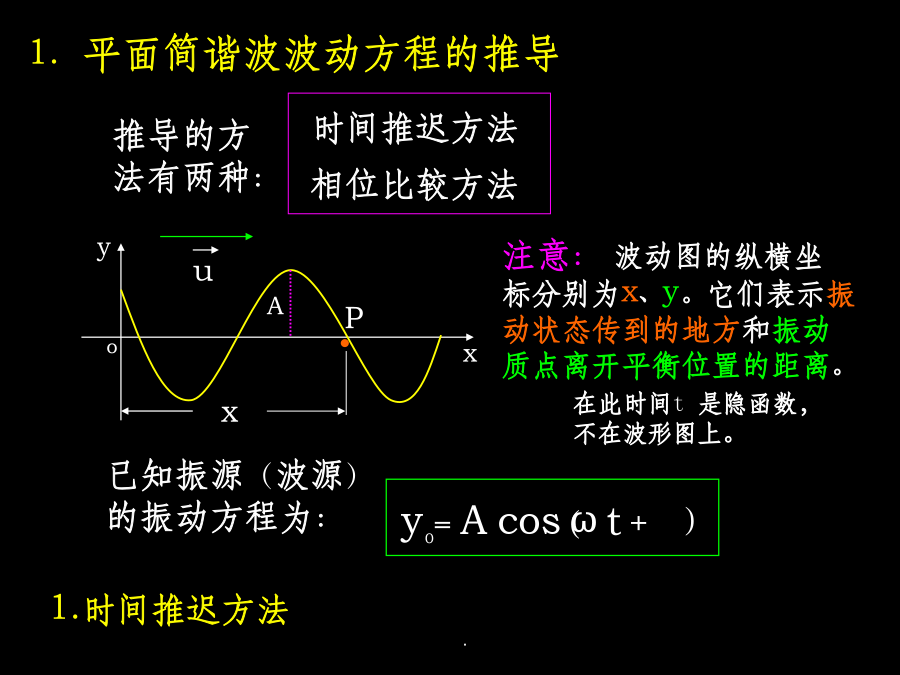
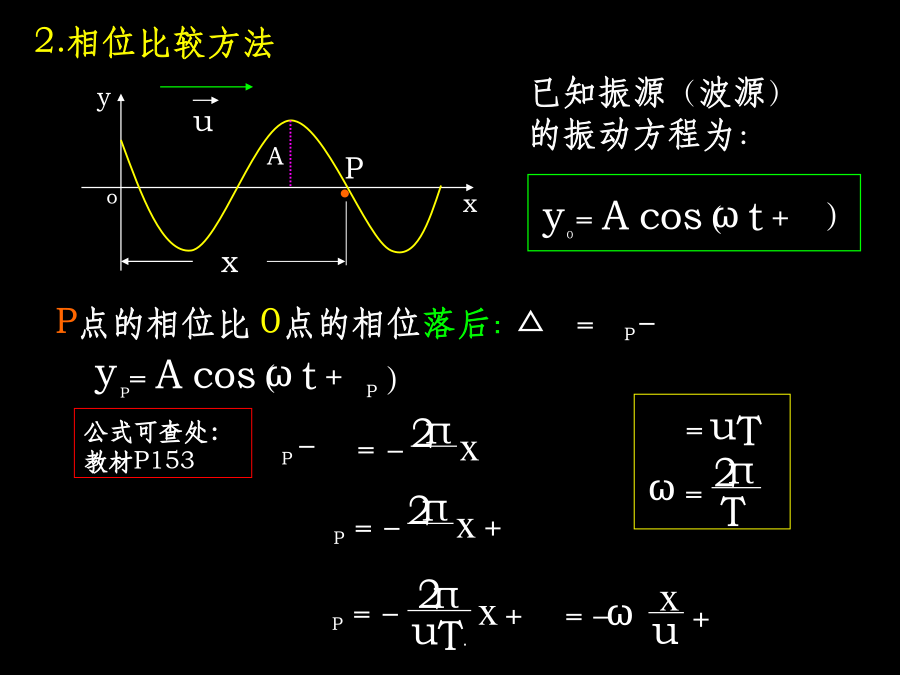
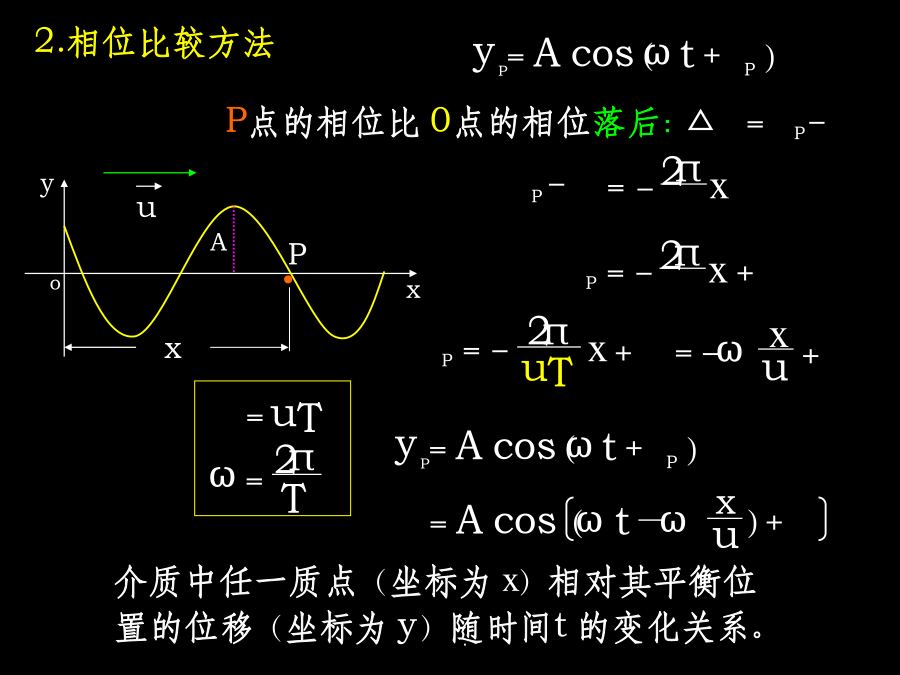
平面简谐波的波函数★简谐波:在均匀的、无吸收的介质中,波源作简谐振动时,其振动状态在介质中传播过程中所形成的波。各种不同的简谐波1.平面简谐波波动方程的推导1.时间推迟方法2.相位比较方法2.相位比较方法波向x轴正方向u角波数:表示单位长度上波的相位变化,在数值上等于2π长度上的完整波数目。解:x例题:图(a)中所表示的x=0处质点振动的初相位与图(b)所表示的振动的初相位分别为:utQ例题:如图所示,为t=0时刻的简谐波形,试求例题:一列沿x正向传播的简谐波,已知t1=0和t2=0.25s时的波形如图。

波动方程ppt课件.ppt
平面简谐波的波函数★简谐波:在均匀的、无吸收的介质中,波源作简谐振动时,其振动状态在介质中传播过程中所形成的波。各种不同的简谐波1.平面简谐波波动方程的推导1.时间推迟方法2.相位比较方法2.相位比较方法波向x轴正方向u角波数:表示单位长度上波的相位变化,在数值上等于2π长度上的完整波数目。解:x例题:图(a)中所表示的x=0处质点振动的初相位与图(b)所表示的振动的初相位分别为:utQ例题:如图所示,为t=0时刻的简谐波形,试求例题:一列沿x正向传播的简谐波,已知t1=0和t2=0.25s时的波形如图。

波动方程与波速ppt课件.ppt
§10.3波动方程与波速§10.3波动方程与波速设横波沿x方向传播,在忽略高级无穷小量时,有——纵波的波动方程对于一维简谐波在密度为,扬氏模量为E的介质传播的纵波的波速公式为理想气体纵波波速(声速)

波动方程与波速ppt课件.ppt
§10.3波动方程与波速§10.3波动方程与波速设横波沿x方向传播,在忽略高级无穷小量时,有——纵波的波动方程对于一维简谐波在密度为,扬氏模量为E的介质传播的纵波的波速公式为理想气体纵波波速(声速)

波动方程举例ppt课件.ppt
三、波动方程举例2变化1一平面简谐波以波速u沿x轴正向传播。位于x=a处的P点的振动方程为波动方程波动方程如波以波速u沿x轴负方向传播,结果如何?例1一平面简谐波以速度沿直线传播,波线上点A的简谐运动方程2)以B为坐标原点,写出波动方程3)写出传播方向上点C、点D的简谐运动方程A2)求波形图.3)处质点的振动规律并做图.例3波动方程100p2.x=2m处3.已知波形图求波动方程o(2)p点处x=0.2m,代入上述波动方程例5沿x轴负方向传播的平面简谐波在t=2s时刻的波形图如图所示,设波速求(1)该波波动
