基于因子分析的logistic违约概率测算模型研究ahre.pdf

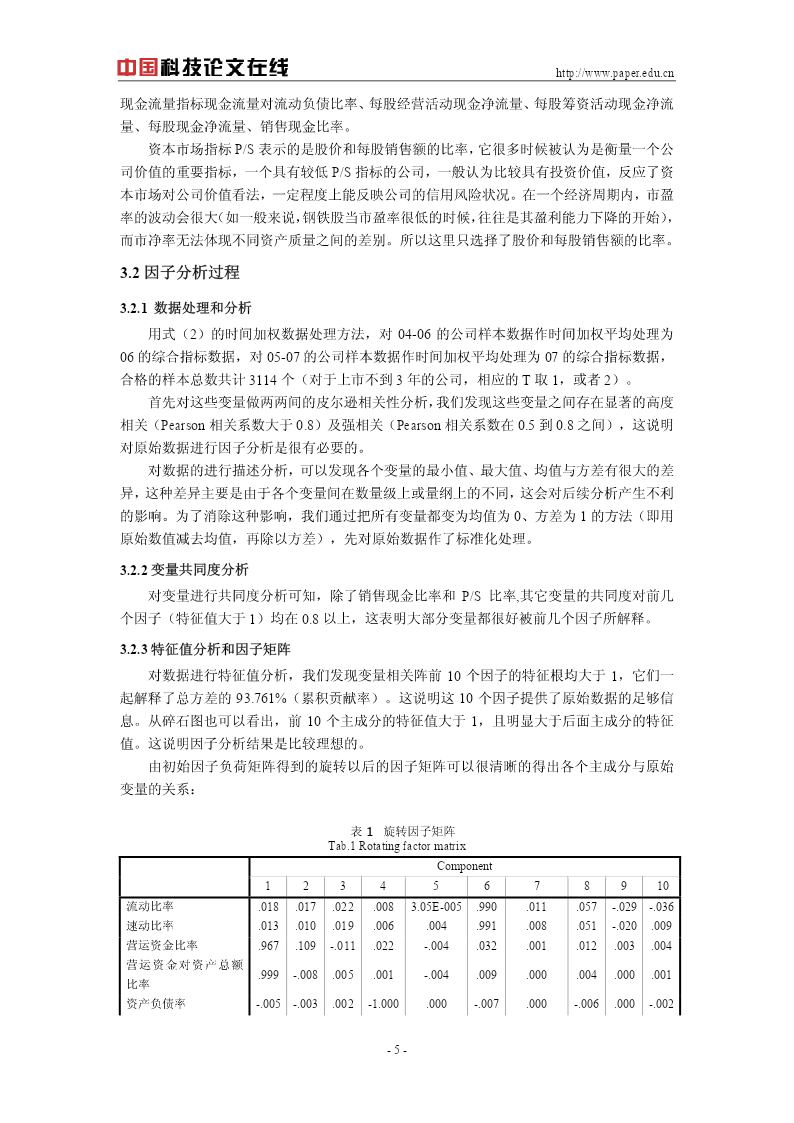
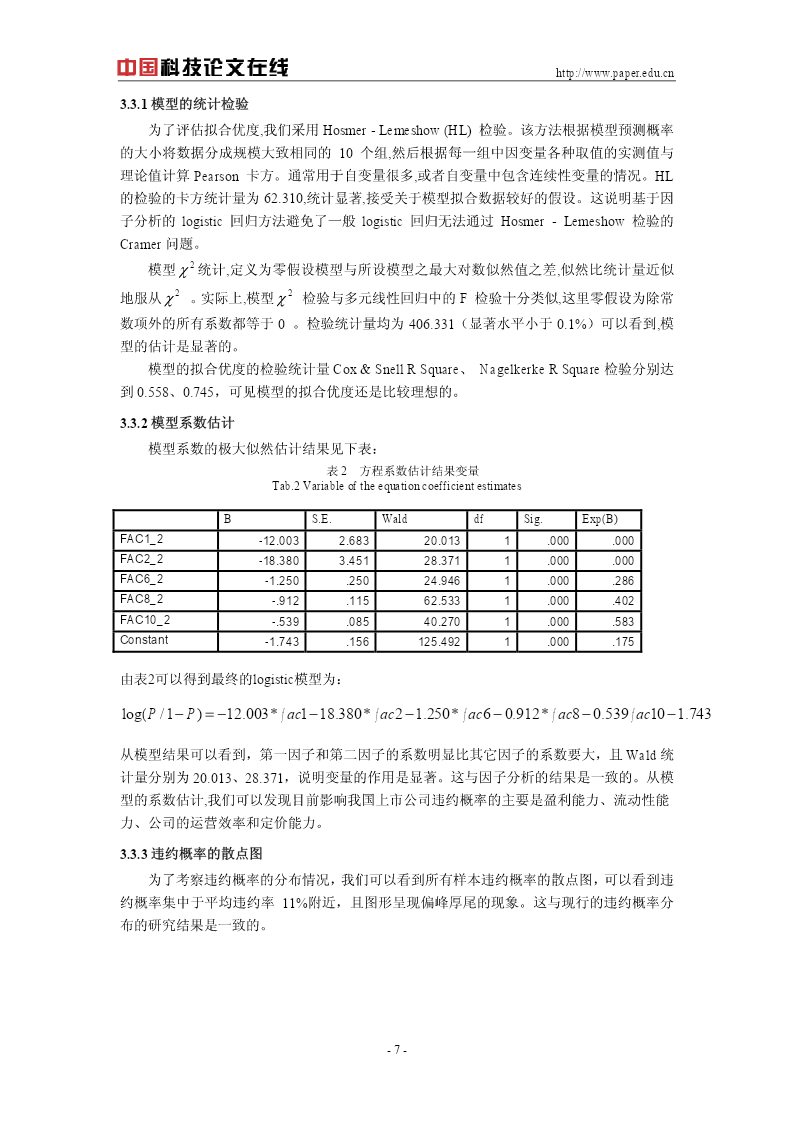
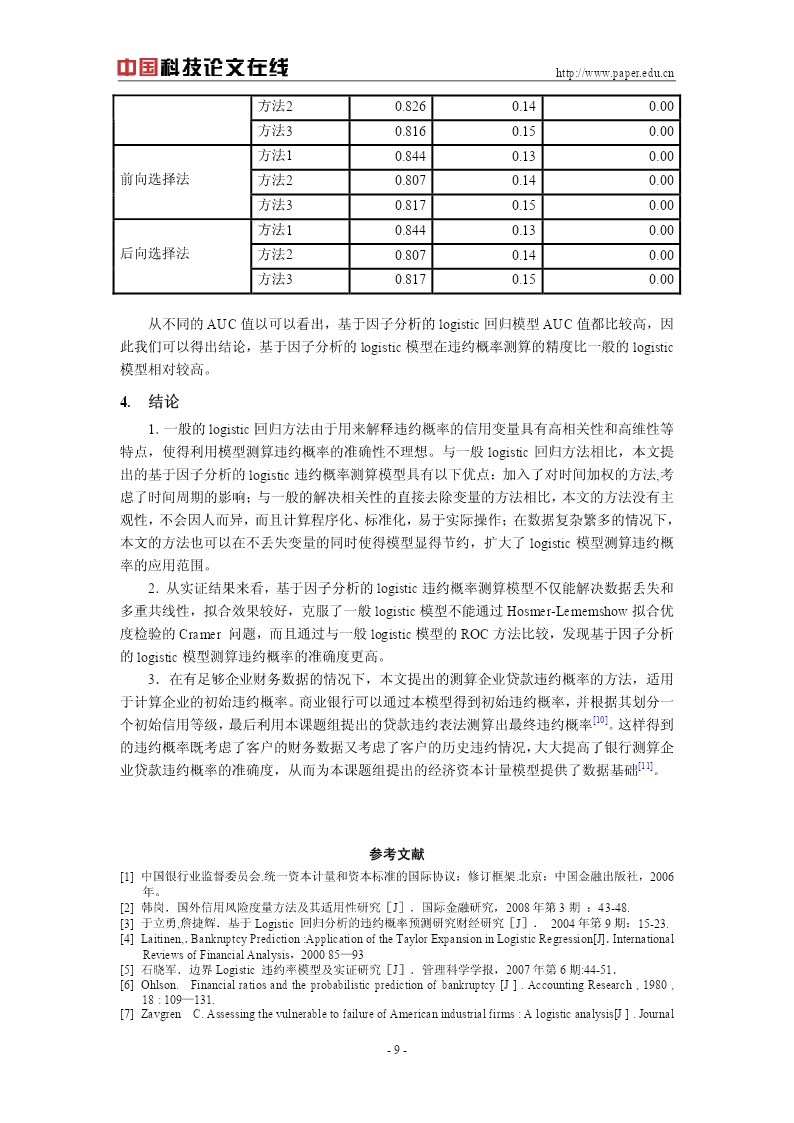
http://www.paper.edu.cn

基于因子分析的logistic违约概率测算模型研究1

彭建刚，屠海波，何婧
湖南大学金融学院，金融管理研究中心，湖南长沙（410079）
E-mail：[e-mail]
摘要：本文针对一般Logistic违约率模型中原始数据信息的丢失、多重共线性以及没有
考虑时间因素等问题，提出了基于因子分析的logistic违约概率测算模型。通过引入因子分
析和对指标作时间加权化处理等方法改进了一般logistic违约概率测算模型，然后利用中国
上市公司数据展开实证研究。基于因子分析的logistic违约概率测算模型不仅考虑了时间因
素，能够解决数据丢失和多重共线性，克服了Cramer问题，而且测算的准确度也较高。
关键词：违约概率，因子分析，Logistic模型
中图分类号：F832.21文献标识码:A

1.引言

美国金融市场近期遭受重创，次级抵押贷款危机已蔓延至全球金融市场。次贷危机起因
于对信用风险没有引起足够的重视，在商业银行信用风险管理中，违约概率的测算居于重要
地位。违约概率是指借款人在未来一定时期内不能按合同要求偿还银行贷款本息或履行相关
义务的可能性(概率)，即信用风险的概率测算。对借款人进行违约概率的测算，己经被列为
巴塞尔新资本协议内部评级法的关键内容，是现代商业银行信用风险管理的重要环节。巴塞
尔新资本协议要求[1]，采用内部评级法的银行必须对处于风险暴露中的每一借款人进行评
级，并估计其违约概率。研究现代商业银行的信用风险管理，不能不关注违约概率测算问题。
20世纪八十年代以来，logistic回归分析法逐步取代了传统的判别分析法。作为量化企
业信用风险的一种主流方法，logistic回归方法不仅灵活简便，而且它的许多前提假设比较符
合经济现实和金融数据的分布规律，譬如它不要求模型变量间具有线性相关关系，不要求变
量服从协方差矩阵相等和残差服从正态分布等，这使得模型的分析结果比较客观。大量实证
研究表明,Logistic模型估计结果与实际数据的拟合度较高,适用性较强[2]。于立勇（2008）[3]
等在结合我国国有商业银行实际数据的基础上通过Logistic回归模型构建了违约概率的测
算模型，实证结果表明,模型可以作为较为理想的违约概率预测工具。
最近对logistic回归方法改进的研究主要有Laitinen（2000）[4]探索了泰勒级数展开在
logistic回归方法预测企业违约分析中的应用。石晓军（2007）[5]则针对一般logistic回归方法
存在的难以通过Hosmer-Lememshow拟合优度检验的Cramer问题，提出了边界logistic方法。
由于用来解释违约概率的信用变量具有高相关性和高维性等特点，使得在运用logistic
回归分析进行企业违约风险预测研究时会影响logistic分析的过程和结果，导致大部分原始
数据信息的丢失以及估计方程中出现共线性的函数关系。而且我国正在处于经济转型时期，
经济发展不够稳定。如果忽视时间因素对违约概率的影响，那么就会造成在经济景气的时期，
商业银行会低估企业违约的概率，从而使得银行面临巨大的信用风险；而在经济萧条阶段又
会高估企业违约的概率，从而使得银行可能失去优质客户。本文正是针对这些问题提出了基
于因子分析的logistic违约概率测算模型，最后用ROC分析检验了不同模型测算违约概率的

1本文得到国家自然科学基金项目(编号:70673021)的资助。

-1-
http://www.paper.edu.cn

精度。
2.基于因子分析的Logistic模型的基本框架

2.1考虑了时间因素的Logistic模型的基本原理
首先利用Logistic模型进行违约概率测算研究的有Ohlson（1980）[6]、Zavgren（1985）[7]
等。Logistic回归分析是一种非线性分类的统计方法,也适用于因变量中存在定性指标的问题,
而且Logistic模型的建立方法---极大似然估计法有很好的统计特性。
在Logistic模型中，违约概率的测算被看作一个虚拟变量问题。所谓虚拟变量指的是一
种取值为0或1的变量。在经济模型中，一些变量比如季节、民族、某项政策等都可能成为
影响某个因变量的重要因素。这些变量所反映的并不是数量，而是某种性质或属性。为了研
究方便，我们人为构造出一种特殊变量，即虚拟变量来把这些变量定量化，规定当该变量值
取1时，表示存在某种性质或属性，取0时则表示不存在。
Logistic模型假设因变量发生的概率与其各影响因素间呈现如下的非线性关系,
1
Π=()X(1)
1+e−+(ββ01122XX+β+....βnnX)
TT
其中XXXX=(,