
《函数的初步认识》.ppt

你的****书屋






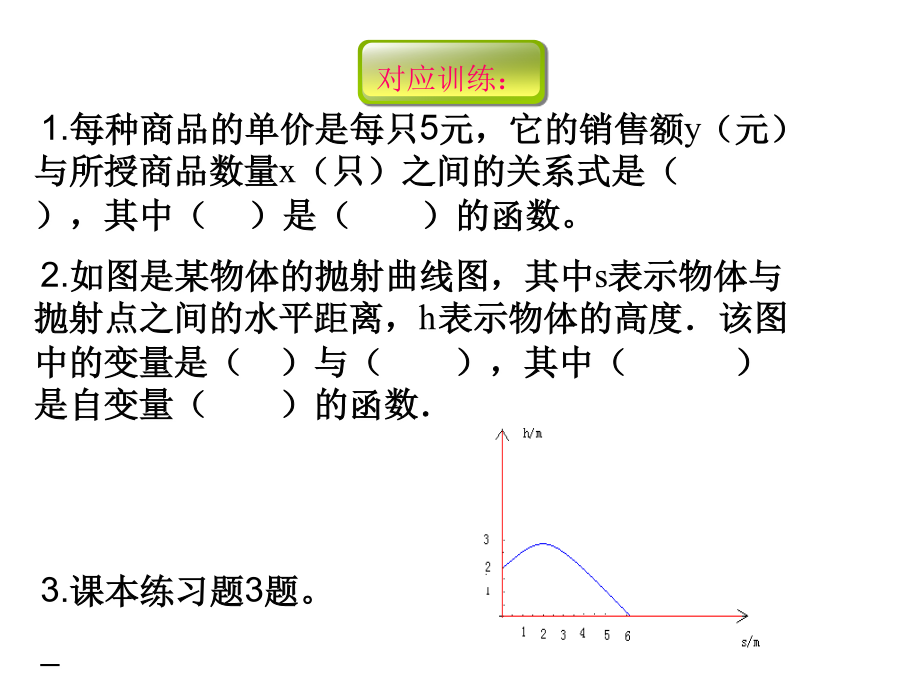

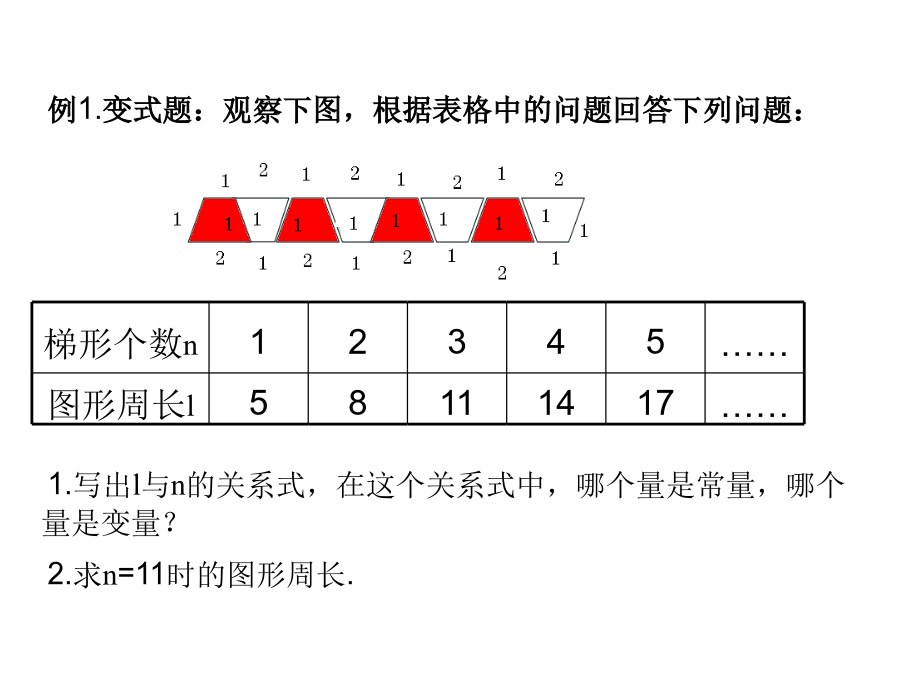

亲,该文档总共13页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

《函数的初步认识》.ppt
§5.5函数的初步认识【知识回顾】1.正方形的周长c与边长a的关系式为_____________,其中常量是________________,变量是___________________.2.如果用r表示圆的半径,S表示圆的面积,则S与r之间满足下列关系:S=__________.利用这个关系式,试求出半径1cm、1.5cm、2cm、2.6cm、3.2cm时圆的面积,并将结果填入下表:1.结合实例,知道自变量与函数的意义,能够区分自变量与函数.2.对于给定的函数,能根据自变量的值求出函数的值.1.自学要求

函数的初步认识.ppt
第十八章函数及其图象复习课在某一变化过程中,可以取不同数值的量,叫做变量。表示函数关系的方法通常有三种:(1)解析法,如观察3中的f=,观察4中的S=πr2,这些表达式称为函数的关系式.求自变量的取值范围(1)分母≠0(2)开偶次方时,被开方数≥0函数相同的条件:在平面上画两条原点重合、互相垂直且具有相同单位长度的数轴(如图),这就建立了平面直角坐标系;O在四个象限及坐标轴上的点的特征:若点P(a,b)在第四象限,则点M(a-b,b-a)在第()象限。点P(3-m,m)是第二象限内的点,则m的取值范围为(

函数的初步认识习题.doc
v1.0可编辑可修改v1.0可编辑可修改v1.0可编辑可修改函数基础一、选择题1、(2010福建泉州市惠安县)函数的自变量的取值范围是()A.B.C.D.2.下列变量之间的关系:①正方体体积V与它的边长a;②x-y=3中的x与y;③y=中的y与x;④圆的面积S与圆的半径r,其中成函数关系的有()A.2个B.3个C.4个D.1个3、(2008沈阳市)函数y=-2x+4当时,的取值范围是()A.B.C.D.4、(08泰州)根据图4中的程序,当输入数值为时,输出数值为()A.4B.6C.8D.10输入输入是否(

函数的初步认识习题.docx
函数基础一、选择题1、(2010福建泉州市惠安县)函数的自变量的取值范围是()A.B.C.D.2.下列变量之间的关系:①正方体体积V与它的边长a;②x-y=3中的x与y;③y=中的y与x;④圆的面积S与圆的半径r,其中成函数关系的有()A.2个B.3个C.4个D.1个3、(2008沈阳市)函数y=-2x+4当时,的取值范围是()A.B.C.D.4、(08泰州)根据图4中的程序,当输入数值为时,输出数值为()A.4B.6C.8D.10输入输入是否(4)(5)5、某企业今年前五个月每个月生产的某种产品的总量C

函数的初步认识习题.doc
函数基础一、选择题1、(2010福建泉州市惠安县)函数的自变量的取值范围是()A.B.C.D.2.下列变量之间的关系:①正方体体积V与它的边长a;②x-y=3中的x与y;③y=中的y与x;④圆的面积S与圆的半径r,其中成函数关系的有()A.2个B.3个C.4个D.1个3、(2008沈阳市)函数y=-2x+4当时,的取值范围是()A.B.C.D.4、(08泰州)根据图4中的程序,当输入数值为时,输出数值为()A.4B.6C.8D.10输入输入是否(4)(5)5、某企业今年前五个月每个月生产的某种产品的总量C
