
河海大学电磁学作业答案1-3.pdf

文库****坚白






亲,该文档总共14页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

河海大学电磁学作业答案.pptx
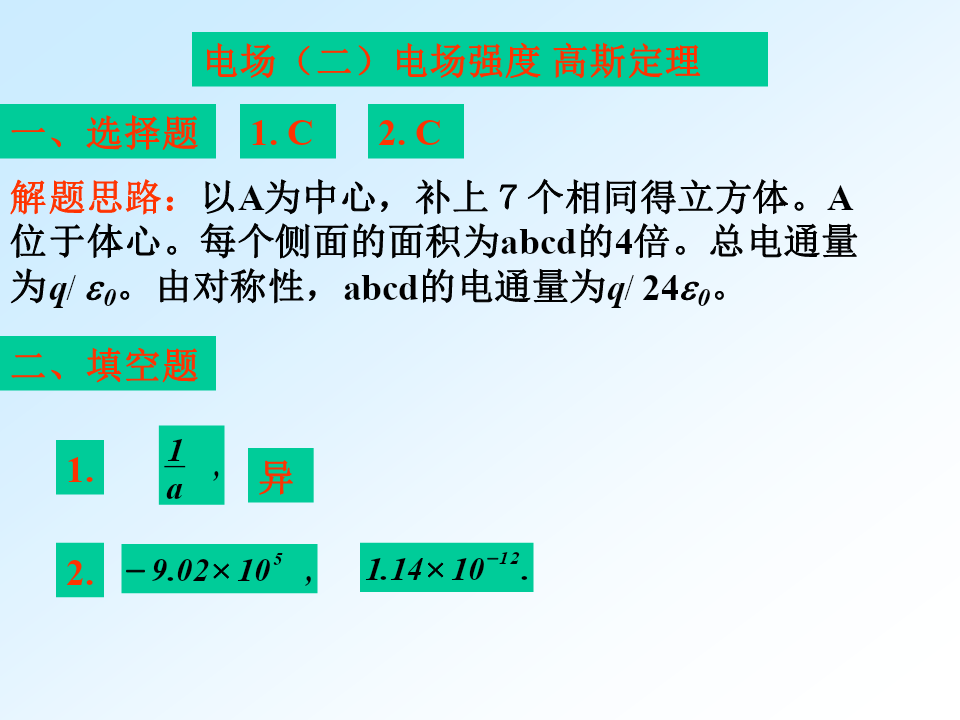
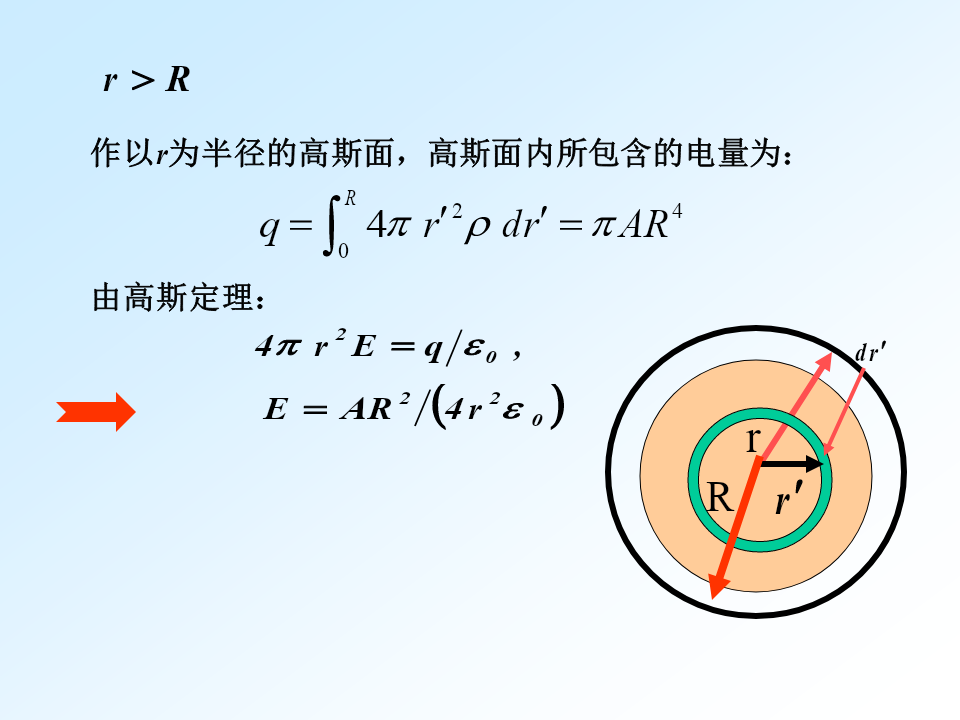
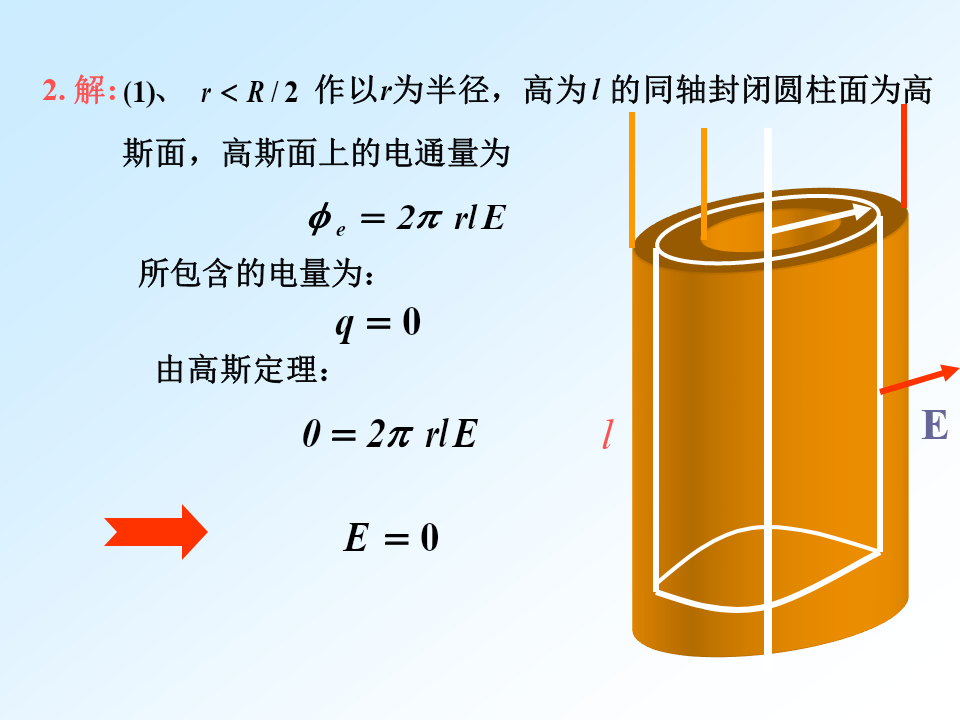
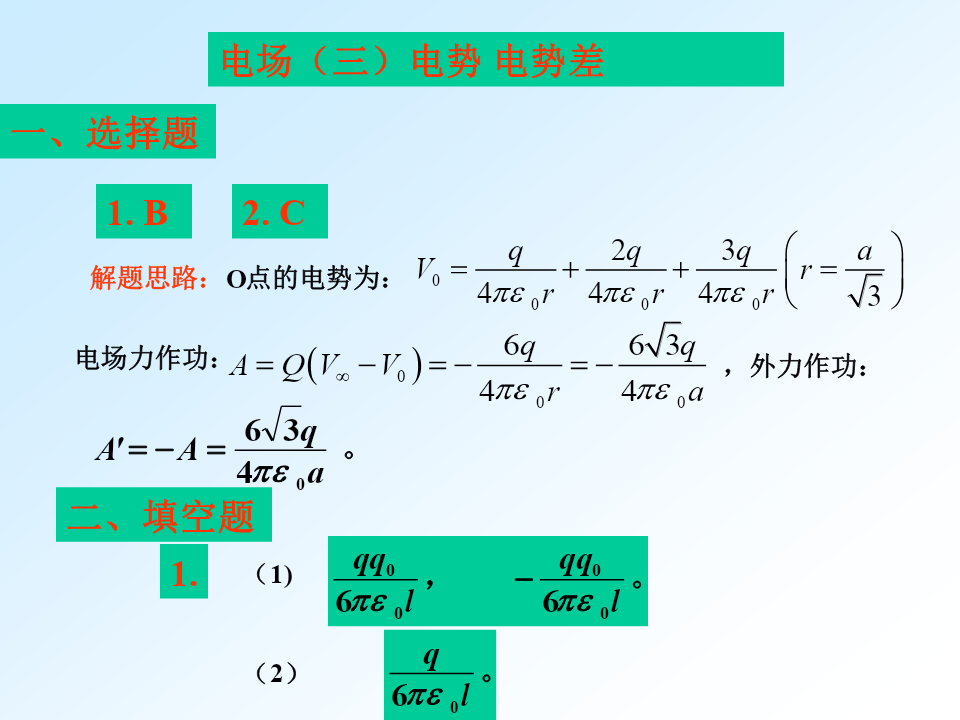
电场(一)库仑定律电场强度三、计算题电场(二)电场强度高斯定理三、计算题作以r为半径的高斯面,高斯面内所包含的电量为:2.解:作以r为半径,高为l的同轴封闭圆柱面为高斯面,高斯面上的电通量为:作以r为半径,高为l的同轴封闭圆柱面为高斯面,高斯面上的电通量为电场(三)电势电势差2.三、计算题对于Q点:(2)2.解:

河海大学电磁学作业答案-磁场.ppt
磁场(一)洛仑兹力磁场(二)安培力磁力的功三、1解B磁场(三)毕萨定理3.三、计算题2.解:磁场(四)安培环路定理00磁场(五)综合练习三、计算题:磁(六)磁介质I3、在一磁感应强度为B的水平的均匀磁场中,有一水平放置的均匀带电的圆盘,电荷面密度为s,半径为R。它围绕其铅直轴线以角速度ω旋转。求它所受到的磁矩和磁力矩。F

河海大学电磁学作业答案6-8.pdf
电场(六)导体aq一、选择题++++Pd11.Db----2.AapEd1qEdd二、填空题p110Sq3,2。1.φb10VφP2.010VbEdd0SqE解题思路:A、B两平板之间为匀强电场00S2.qRφp,Ep0,qA0,φ'p0,E'p0,q'Aq.4πε0rr解题思路:A球不接地、由于静电感应,A球表面分布感应电荷。但总电量为0。球内电场为0。球是等势体。P点的电势和O点的电势相等,O点的电势可以看作q在O点电势和A上感应电荷在
河海大学电磁学作业答案4-5.ppt
电场(四)电势电势梯度、电场能量(4)由此可得:2、电场(五)综合练习一2.4.解:2、一半径为“无限长”圆柱形带电体,其电荷密为=Ar(R>r),式中A为常数,求:(1)、圆柱体内外的场强分布;(2)、选距离轴线为l(l>R)处的电势为零,计算电势分布、由高斯定理可得(1)

河海大学电磁学作业答案6-8.pptx
电场(六)导体2.3.(3).在外球壳带电为-q的基础上,内球壳接地后,电场(七)电介质和电容二、填空题电压:3.4.三、计算题2.解法一:电场(八)综合练习二2.B二、填空题解题思路:并联电容上电压相同,电量分配与电容量成正比:三、计算题
