
圆方程专题培训市公开课金奖市赛课一等奖课件.pptx

lj****88








亲,该文档总共51页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

圆方程专题培训市公开课金奖市赛课一等奖课件.pptx
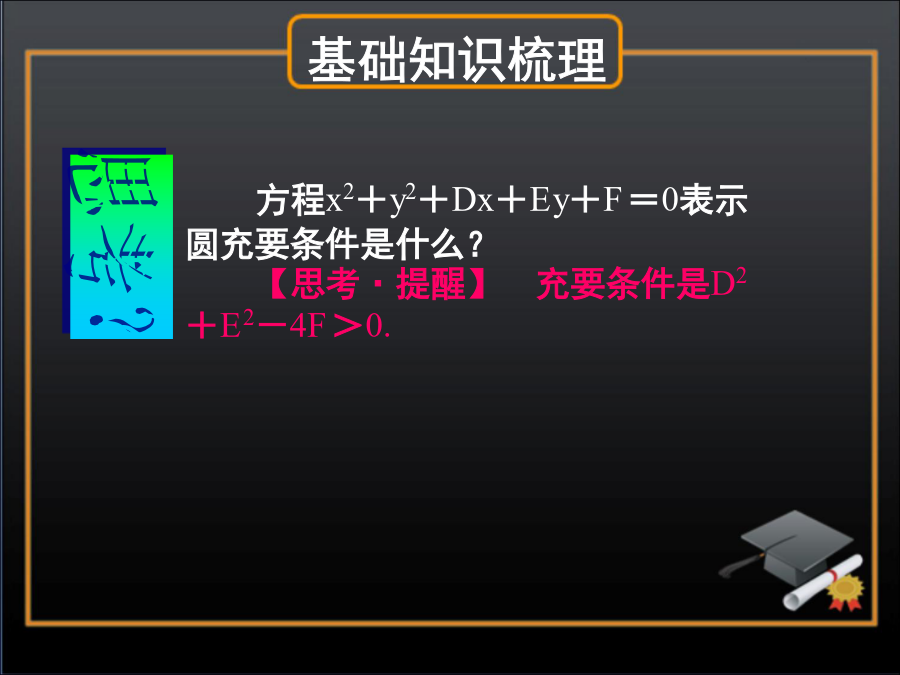
第3学时圆方程1.圆定义(1)在平面内,到定点距离等于点集合叫做圆.(2)拟定一个圆要素是和.2.圆方程方程x2+y2+Dx+Ey+F=0表示圆充要条件是什么?【思考·提醒】充要条件是D2+E2-4F>0.1.方程a2x2+(a+2)y2+2ax+a=0表示圆,则()A.a=-1B.a=2C.a=-1或2D.a=1答案:A2.(高考重庆卷改编)圆心在x轴上,半径为1,且过点(2,1)圆方程是()A.y2+(x-2)2=1B.x2+(y-2)2=1C.(x-1)2+(y-3)2=1D.x2+(y-3)2=1
圆方程专题培训市公开课金奖市赛课一等奖课件.pptx
第3学时圆方程1.圆定义(1)在平面内,到定点距离等于点集合叫做圆.(2)拟定一个圆要素是和.2.圆方程方程x2+y2+Dx+Ey+F=0表示圆充要条件是什么?【思考·提醒】充要条件是D2+E2-4F>0.1.方程a2x2+(a+2)y2+2ax+a=0表示圆,则()A.a=-1B.a=2C.a=-1或2D.a=1答案:A2.(高考重庆卷改编)圆心在x轴上,半径为1,且过点(2,1)圆方程是()A.y2+(x-2)2=1B.x2+(y-2)2=1C.(x-1)2+(y-3)2=1D.x2+(y-3)2=1

圆的面积专题培训市公开课金奖市赛课一等奖课件.pptx
圆的面积将圆转化成什么样图形来推导它面积计算公式呢?把圆分成32份,拼后图形就比较靠近长方形了。假如把圆分份数越多,拼成图形就越靠近长方形了。圆周长=πd长方形面积=长×宽2.一个圆半径是10分米,它面积是多少平方分米?3.一块圆形铁片直径为12毫米,这块铁片面积是多少平方毫米?4.街心花园中圆形花坛周长是18.84米。花坛面积是多少平方米?2、一个雷达屏幕直径是40厘米,它面积是多少平方厘米?3、判断对错:3、判断对错:3、判断对错:3、判断对错:思考题:求下列名图形阴影部分面积。(单位:厘米)做一做:

圆奥秘专题培训市公开课金奖市赛课一等奖课件.pptx
一至六单元复习一、圆奥秘1、到定点距离等于定长点集合叫圆在同一个圆里,直径长度是半径2倍,能够表示为d=2r或r=d/2.公式:圆周长公式C=兀d或C=2兀r圆面积公式S=兀r×r圆柱体积V=兀r×rh惯用数据问题回答4、车轮为何都是圆形呢?由于圆心到地面距离是半径,半径不变,因此平稳。5、人们在围观时,为何会自然地围成圆形呢?由于围成圆时半径都相等,每个人看表演距离都同样,很公平,并且围成圆,演员活动范围很大,看表演时视角很大。半圆的知识圆的对称性图形名称错题分析:一根圆柱形木棒半径是5厘米,在上面缠绕

圆奥秘专题培训市公开课金奖市赛课一等奖课件.pptx
一至六单元复习一、圆奥秘1、到定点距离等于定长点集合叫圆在同一个圆里,直径长度是半径2倍,能够表示为d=2r或r=d/2.公式:圆周长公式C=兀d或C=2兀r圆面积公式S=兀r×r圆柱体积V=兀r×rh惯用数据问题回答4、车轮为何都是圆形呢?由于圆心到地面距离是半径,半径不变,因此平稳。5、人们在围观时,为何会自然地围成圆形呢?由于围成圆时半径都相等,每个人看表演距离都同样,很公平,并且围成圆,演员活动范围很大,看表演时视角很大。半圆的知识圆的对称性图形名称错题分析:一根圆柱形木棒半径是5厘米,在上面缠绕
