预览加载中，请您耐心等待几秒...

动力学普遍方程及拉格朗日方程.ppt

预览
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10

亲，该文档总共51页，到这已经超出免费预览范围，如果喜欢就直接下载吧～

下载提示 文本预览

如果您无法下载资料，请参考说明：

1、部分资料下载需要金币，请确保您的账户上有足够的金币

2、已购买过的文档，再次下载不重复扣费

3、资料包下载后请先用软件解压，在使用对应软件打开

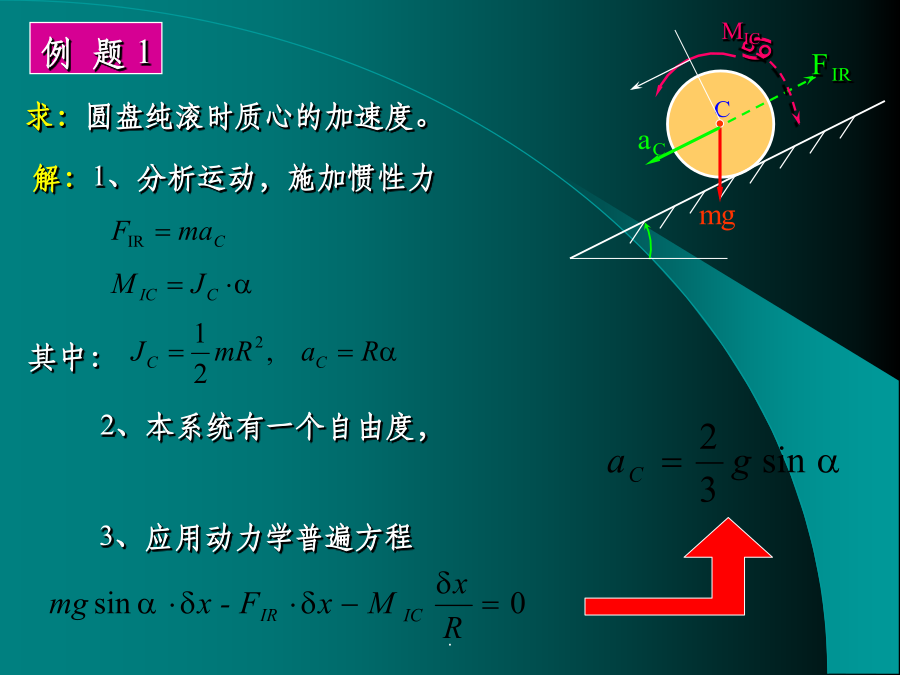
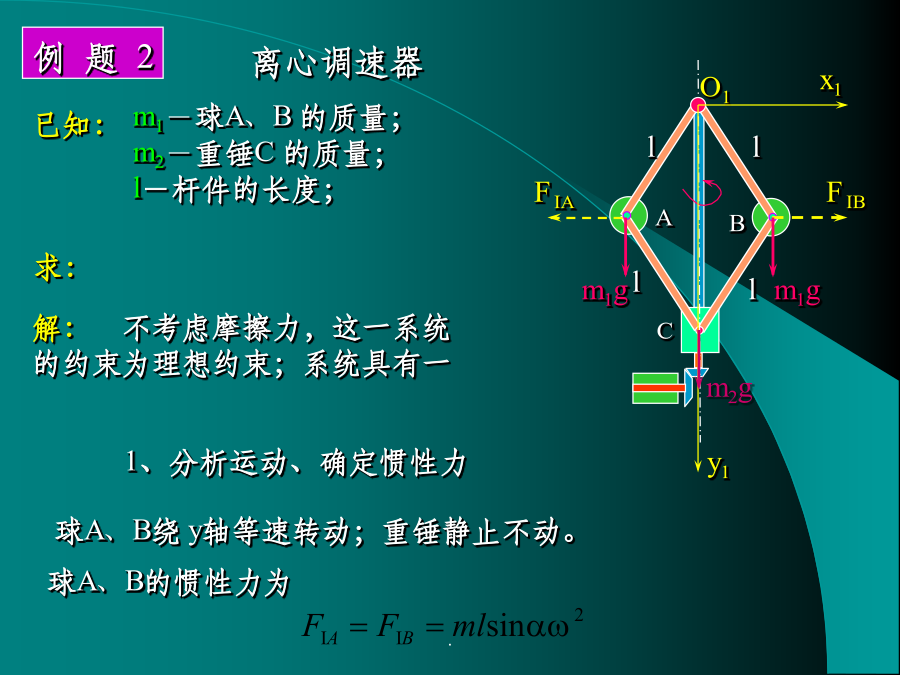
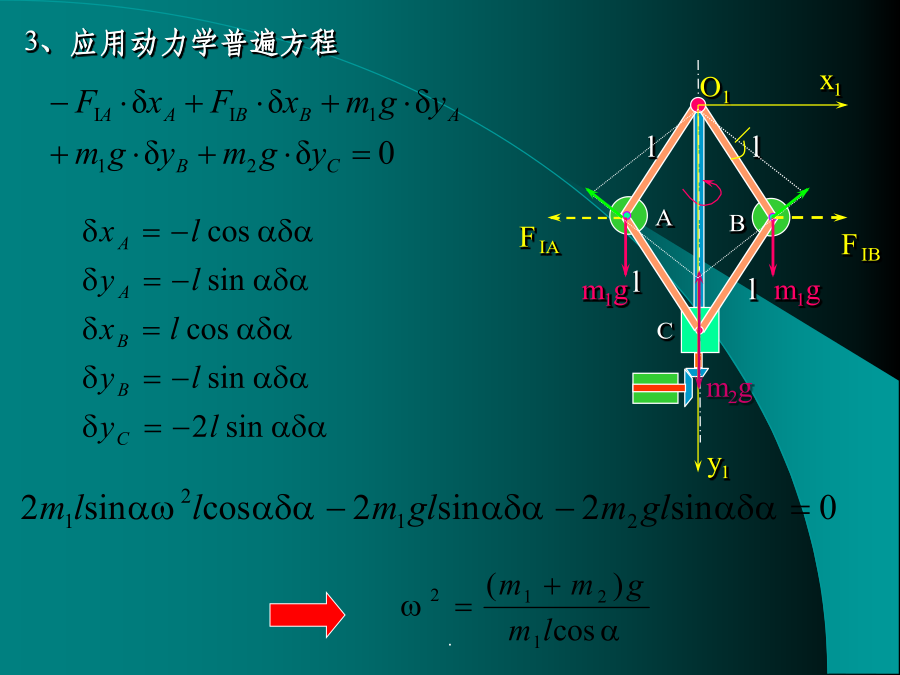
动力学普遍方程 和拉格朗日方程经典动力学的两个发展方面考察由N个质点的、具有理想约束的系统。根据 达朗贝尔原理，有系统的总虚功为动力学普遍方程的直角坐标形式动力学普遍方程主要应用于求解动力学第二类问 题，即：已知主动力求系统的运动规律。例题1例题2xxxx解：5、求解联立方程拉格朗日(Lagrange)方程.第一个Lagrange经典关系(消点)对任意一个广义坐标qj求偏导数此即拉格朗日方程，或称为第二类拉格朗日方程。引入拉格朗日函数对于只具有完整约束、自由度为N的系统，可以得到 由N个拉格朗日方程组成的方程组。OO例题54、应用拉格朗日方程例题6xx..OOO..O1O1O1O1..拉格朗日(Lagrange)方程的初积分O1O1结论与讨论达朗贝尔原理在形式上将质点系动力学问题化为静力学平衡问题。第一类拉格朗日方程，即达朗贝尔－拉格朗日方程，又称为动力学普遍方程。第二类拉格朗日方程:仅用动能、势能以及广义主动力等少数几个标量便可描述复杂质点系的运动。但只能用于具有完整约束的系统。结论与讨论