计量经济学-多元线性回归模型及参数估计.ppt

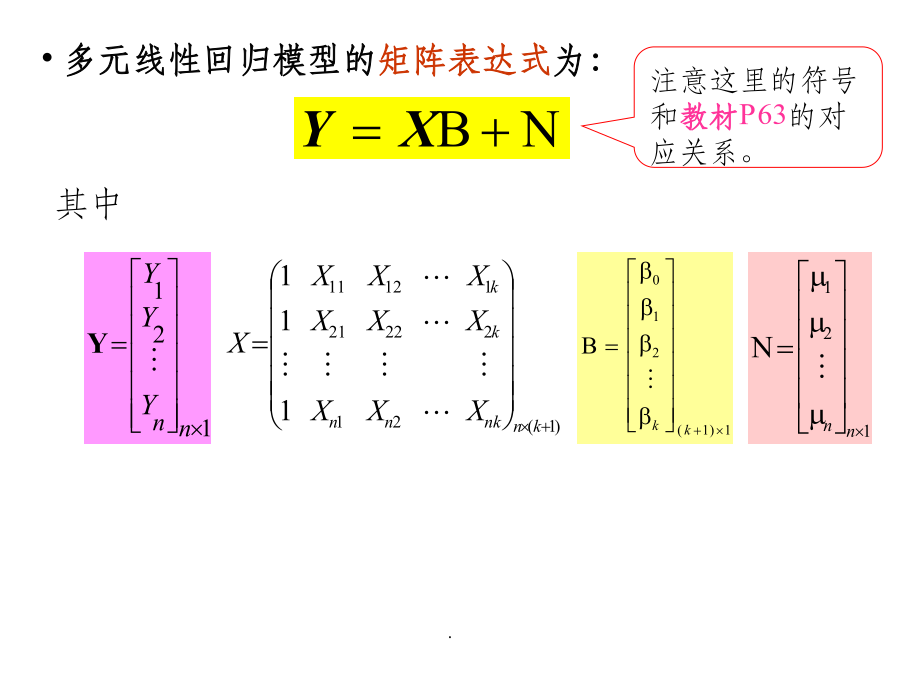
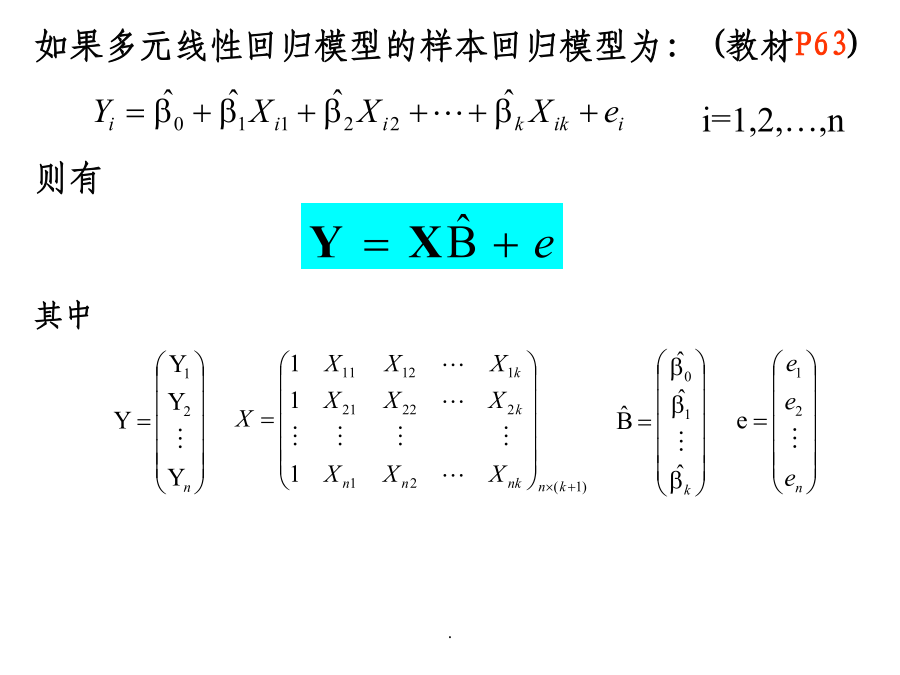
第三章经典单方程计量经济学模型：多元线性回归模型本章主要内容§3.1多元线性回归模型及其参数估计由于：
在实际经济问题中，一个变量往往受到多个原因变量的影响；
“从一般到简单”的建模思路。
所以，线性回归模型中的解释变量往往有多个（至少开始是这样）。这样的模型被称为多元线性回归模型。多元线性回归模型的一般形式为：多元线性回归模型的矩阵表达式为：其中2.多元线性回归模型的基本假定(见教材P64-65)（4）随机误差项具有零均值和同方差；随机误差项在不同样本点之间是独立的，不存在序列相关：
E(i)=0i=1,2,…,n
Var(i)=2i=1,2,…,n
Cov(i,j)=0i≠ji,j=1,2,…,n（5）随机误差项与解释变量之间不相关：
Cov(Xij,i)=0i=1,2,…,n；j=1,2,…,k
（6）随机误差项服从零均值、同方差、零协方差的正态分布：
i~N(0,2)i=1,2,…,n2.多元线性回归模型的基本假定（矩阵形式）2.多元线性回归模型的基本假定（矩阵形式）2.多元线性回归模型的基本假定（矩阵形式）1.普通最小二乘估计根据最小二乘原理，参数估计值应该是下列方程组的解：于是得到关于待估参数估计值的正规方程组：上述估计过程的矩阵表示求解过程如下：（教材P66）于是，得到正规方程组：例利用第二版P28表2.1.3中的家庭可支配收入（X）和消费支出（Y），估计一元线性回归模型，参数估计的计算可通过下面的表2.2.1进行。因此，由该样本估计的回归方程为：对于该例题，如果用矩阵公式求解，那么过程如下：例3.2.1⃟正规方程组的另一种写法：(教材P67)离差形式的样本回归方程随机误差项的均值为0，方差的无偏估计量为：随机误差项方差估计量的无偏性（证明，有补充，不要求）其中,符号“tr”表示矩阵的迹，其定义为矩阵主对角线元素的和。注：潘文卿等《计量经济学学习指南与练习》P50给出了另一种证明。2.最大似然估计（MaximumLikelihood,ML)(不作要求）对数似然函数为

参数的最大似然估计

结果与参数的普通最小二乘估计相同。3.矩估计（MomentMethod,MM）（不作要求）三、OLS参数估计量的统计性质（教材P70）1．线性3．有效性.根据高斯—马尔可夫定理，上述方差在所有无偏估计量的方差中是最小的，所以普通最小二乘参数估计量具有有效性。四、样本容量问题⒈最小样本容量（教材P71）2.满足基本要求的样本容量（教材P71）五、多元线性回归模型实例（一）中国居民人均消费模型——二元线性回归模型第二版教材P50表2.5.1中国居民人均消费支出与人均GDP（元/人）Eviews软件运行结果拟合效果（二）第三版教材P72-73例3.2.2第三版教材P72-73例3.2.2