沃尔什哈达玛变换ppt课件.ppt

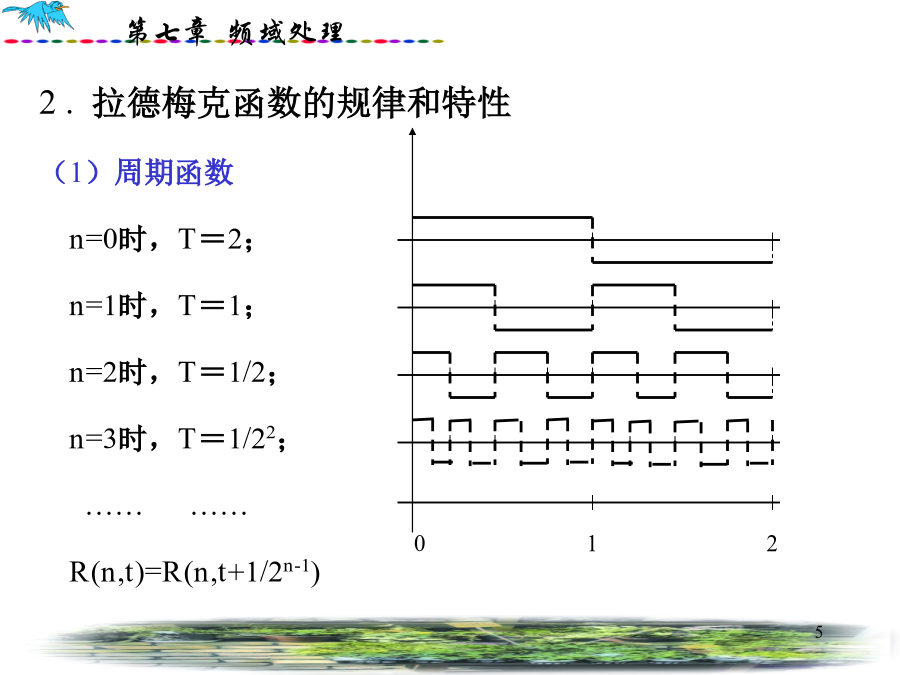
7.5离散沃尔什-哈达玛变换
（WalshHadamardTransform）（2）格雷码到二进制的转换：7.5.2拉德梅克函数（Rademacher）

1.拉德梅克函数定义

可见，R(n,t)为周期函数。

2.拉德梅克函数的规律和特性
（1）周期函数
n=0时，T＝2；
n=1时，T＝1；
n=2时，T＝1/2；
n=3时，T＝1/22；
…………
R(n,t)=R(n,t+1/2n-1)（2）函数的取值
R(n,t)的取值只有＋1和－1。
（3）函数的频率特性
R(n,t)是R(n－1,t)的二倍频。
（4）函数离散化
如果已知n，则R(n,t)在（0<t<1）范围内有2n-1个周期。（连续）
若在t=(k+1/2)/2n处作取样，则可得到一个离散的数据序列R(n,k)，其中，k=0,1,2……2n-1。（离散）7.5.3沃尔什函数（Walsh）

沃尔什函数有三种不同的函数定义，但都可由拉德梅克函数构成。

例：当p＝3时，对前8个Walw(i,t)取样，则：

Walw(0,t)=1——{1,1,1,1,1,1,1,1}
Walw(1,t)=R(1,t)——{1,1,1,1,-1,-1,-1,-1}
Walw(2,t)=R(1,t)R(2,t)——{1,1,-1,-1,-1,-1,1,1}
Walw(3,t)=R(2,t)——{1,1,-1,-1,1,1,-1,-1}
Walw(4,t)=R(2,t)R(3,t)——{1,-1,-1,1,1,-1,-1,1}
Walw(5,t)=R(1,t)R(2,t)R(3,t)——{1,-1,-1,1,-1,1,1,-1}
Walw(6,t)=R(1,t)R(3,t)——{1,-1,1,-1,-1,1,-1,1}
Walw(7,t)=R(3,t)——{1,-1,1,-1,1,-1,1,-1}取样后得到的按沃尔什排列的沃尔什函数矩阵（2）按佩利（Paley）排列的沃尔什函数例：当p＝3时，对前8个Walp(i,t)取样，则：

Walp(0,t)=1——{1,1,1,1,1,1,1,1}
Walp(1,t)=R(1,t)——{1,1,1,1,-1,-1,-1,-1}
Walp(2,t)=R(2,t)——{1,1,-1,-1,1,1,-1,-1}
Walp(3,t)=R(1,t)R(2,t)——{1,1,-1,-1,-1,-1,1,1}
Walp(4,t)=R(3,t)——{1,-1,1,-1,1,-1,1,-1}
Walp(5,t)=R(1,t)R(3,t)——{1,-1,1,-1,-1,1,-1,1}
Walp(6,t)=R(2,t)R(3,t)——{1,-1,-1,1,1,-1,-1,1}
Walp(7,t)=R(1,t)R(2,t)R(3,t)——{1,-1,-1,1,-1,1,1,-1}取样后得到的按佩利排列的沃尔什函数矩阵（3）按哈达玛（Hadamard）排列的沃尔什函数例：当p＝3时，对前8个WalH(i,t)取样，则：

WalH(0,t)=1——{1,1,1,1,1,1,1,1}
WalH(1,t)=R(3,t)——{1,-1,1,-1,1,-1,1,-1}
WalH(2,t)=R(2,t)——{1,1,-1,-1,1,1,-1,-1}
WalH(3,t)=R(2,t)R(3,t)——{1,-1,-1,1,1,-1,-1,1}
WalH(4,t)=R(1,t)——{1,1,1,1,-1,-1,-1,-1}
WalH(5,t)=R(1,t)R(3,t)——{1,-1,1,-1,-1,1,-1,1}
WalH(6,t)=R(1,t)R(2,t)——{1,1,-1,-1,-1,-1,1,1}
WalH(7,t)=R(1,t)R(2,t)R(3,t)——{1,-1,-1,1,-1,1,1,-1}取样后得到的按哈达玛排列的沃尔什函数矩阵2n阶哈达玛矩阵有如下形式：可见，哈达玛矩阵的最大优点在于它具有简单的递推关系，即高阶矩阵可用两个低阶矩阵的克罗内克积(KroneckerProduct)求得。因此常采用哈达玛排列定义的沃尔什变换。7.5.4离散沃尔什－哈达玛变换（DWHT）
和由哈达玛矩阵的特点可知，沃尔什-哈达玛变换的本质上是将离散序列f(x)的各项值的符号按一定规律改变后，进行加减运算，因此，它比采用复数运算的DFT和采用余弦运算的DCT要简单得多。例：将一维信号序列﹛0，0，1，1，0，0，1，1﹜作WHT变换及反变换。二维离散沃尔什变换
很容易将一维WHT的定义推广到二维WHT。二维WHT的正变换核和逆变换核分别为例：二维离散沃尔什变换的矩阵形式表达式为M=N=4，其二维WHT变换核为所以26二维WHT结果
（a）原图像（b）WHT结果
从