齐次线性方程组有非零解的条件及解的结构市公开课一等奖省赛课获奖PPT课件.pptx

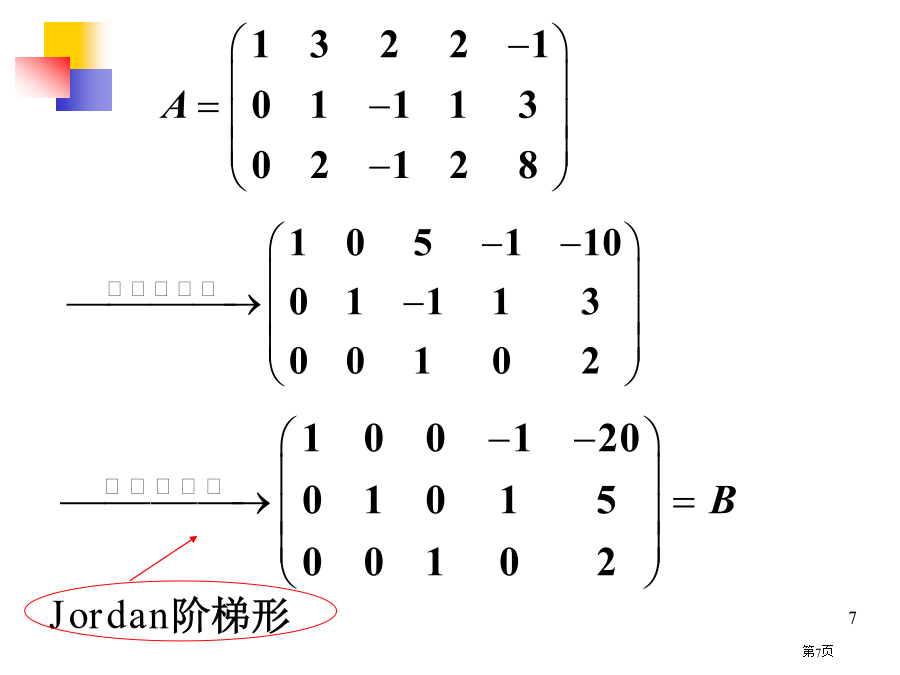
§4.5齐次线性方程组有非零解条件及解结构定理8设A为s×n矩阵,则齐次线性方程组AX=0有非零解充要条件为rA<n.齐次线性方程组解性质：恰好就是AX=0解集合,称
k1X1+k2X2+...+ktXt为AX=0通解.Jordan阶梯形现解AX=0同解齐次线性方程组BX=0.Jordan阶梯形B有3行不为零，故rB=3，定理9设A是s×n矩阵,rA=r<n,则齐次线性方程组AX=0存在基础解系,且基础解系含n－r个解向量.未知量xr+1,xr+2,...,xn(都不在首元所在
列)称为自由未知量.BX=0为AX=0同解
方程组.令自由未知变量为BX=0一个解.再令自由未知变量xr+1,...,xn值分别为(0,1,...,0),...,(0,0,...,1),代入BX=0可解得BX=0解X2,X3,...,Xn－r,16说明：上述定理证实过程实际上就是求解齐次线性方程组步骤.解:用基础解系表示全部解为推论设齐次线性方程组AX=0系数矩阵A为s×n矩阵，若rA=r<n,则证实：设X1,X2,...,Xn－r(I)为AX=0一个基础解系.设(III)为AX=0任意
线性无关解,为AX=0任意解,则
线性相关，于是可
由(III)线性表出，故(III)为AX=0一个
基础解系.例3设A为s×n矩阵,B为n×m矩阵,AB=0,则rA+rB≤n.于是为AX=0解.例(P85.Q3)设A为n(n≥2)阶方阵,证实:(2)若rA<n－1,则知全部n－1阶子式全
部为零，所以A余子式也为零，从而
A*=0，也即