编译原理习题与答案市公开课一等奖省赛课微课金奖PPT课件.pptx

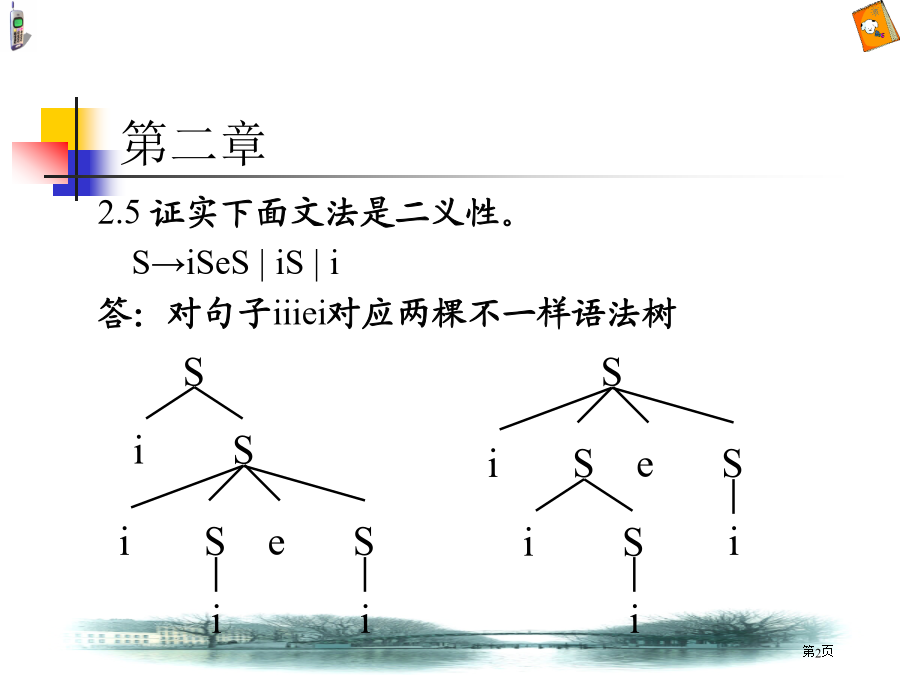
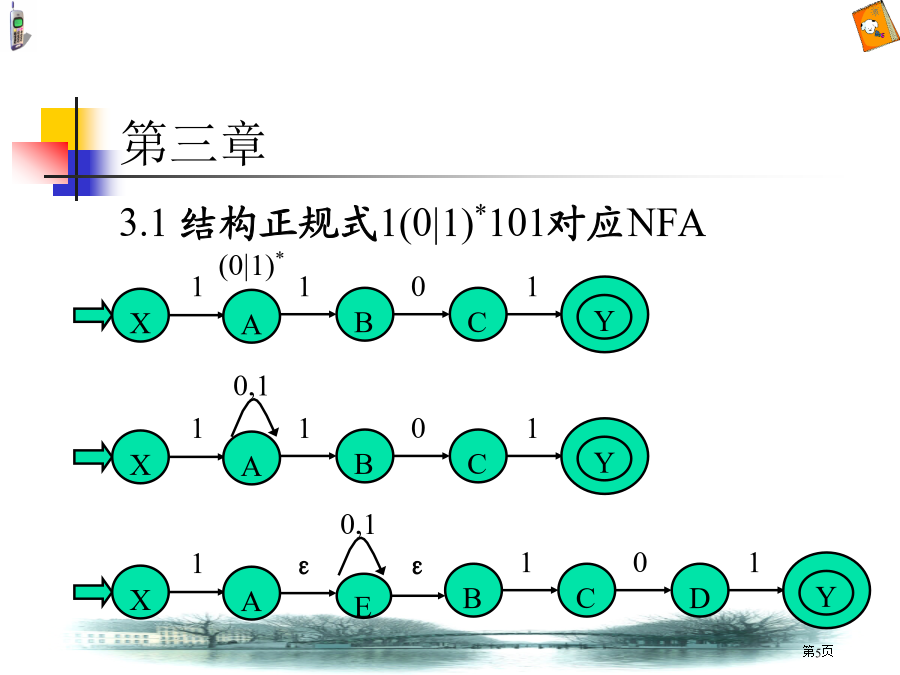
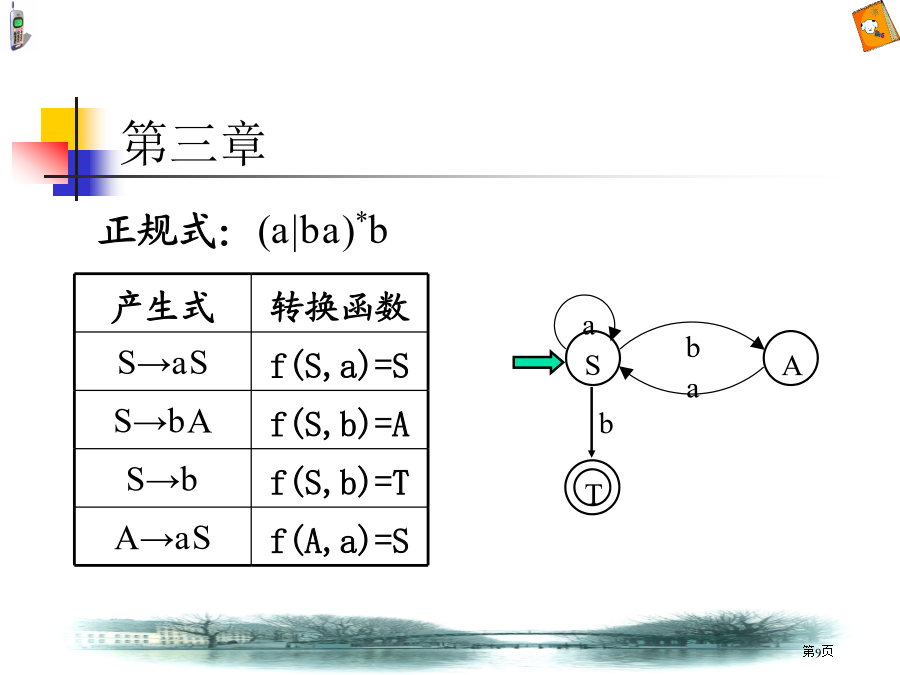
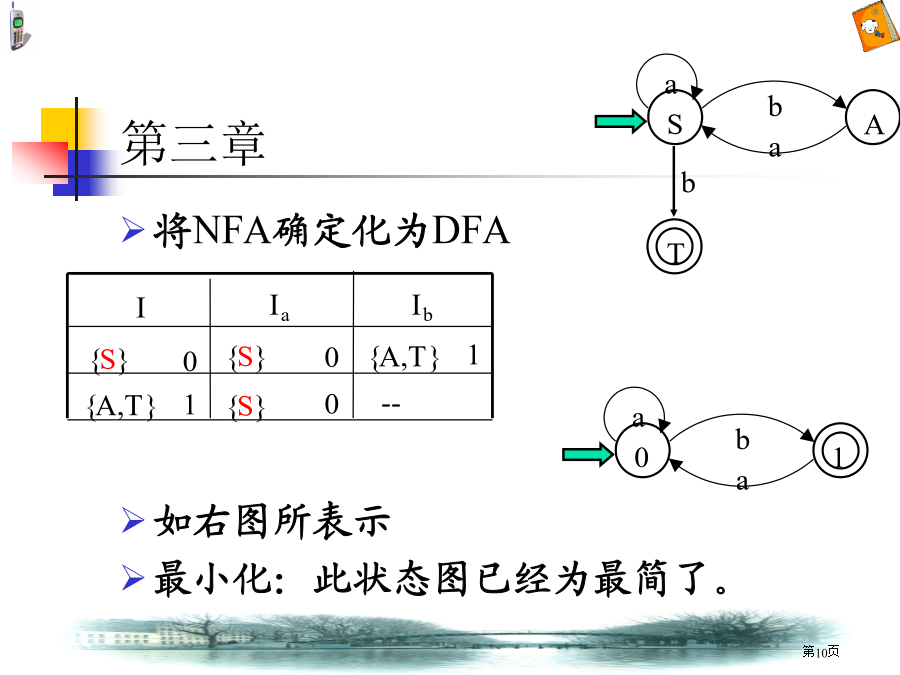
第二章2.5证实下面文法是二义性。
S→iSeS|iS|i
答：对句子iiiei对应两棵不一样语法树2.9设有文法G[T]:T→T*F|F F→FîP|P P→(T)|i
分析句型T*Pî(T*F)短语、直接短语和句柄
答：句型T*Pî(T*F)语法树：第三章第三章第三章3.4给出文法G[S]，结构对应最小DFA。
G：S→aS|bA|bA→aS
解：由文法到NFA转换有两种方法：
①由文法到正规式，再由正规式到NFA
先由产生式得: A=aS
将A代入S中得: S=aS|bA|b=aS|baS|b
=(a|ba)S|b
利用规则（A->xA|y）得: S=(a|ba)*b
文法G对应正规式为(a|ba)*b，其对应NFA状态转换图为：第三章第三章第三章第三章第三章第三章第三章第三章第三章上图所对应DFA以下所表示。对上图DFA进行最小化。首先将状态分为非终态集和终态集两部分：{0,1,2,5}和{3,4,6,7}。
由终态集可知，对于状态3、6、7，不论输入字符是a还是b下一状态均为终态集，而状态4在输入字符b下一状态落入非终态集，故将其化为分{0,1,2,5},{4},{3,6,7}第三章6.设有L(G)={a2n+1b2ma2p+1|n≥0,p≥0,m≥1}。
(1)给出描述该语言正规表示式；
(2)结构识别该语言确实定有限自动机(可直接用状态图形式给出)。
解：
(1)该语言对应正规式为a(aa)*bb(bb)*a(aa)*。
(2)a(aa)*bb(bb)*a(aa)*正规表示式对应NFA如下图所表示。第三章 重新命名后状态转换矩阵可化简为(可由最小化方法得到)
{X,2}{1}{3,5}{4}{6}{Y}
按次序重新命名为0、1、2、3、4、5后得到最简DFA，以下列图所表示。 7.有一台自动售货机，接收1分和2分硬币，出售3分钱一块硬糖。用户每次向机器中投放≥3分硬币，便可得到一块糖(注意：只给一块而且不找钱)。
(1)写出售货机售糖正规表示式；
(2)结构识别上述正规式最简DFA。
解：(1)设a=1，b=2，则售货机售糖正规表示式为
a(b|a(a|b))|b(a|b)。
(2)画出与正规表示式a(b|a(a|b))|b(a|b)对应NFA，如图所表示。由转换矩阵可看出，非终态2和非终态3面对输入符号a或b下一状态相同，故合并为一个状态
即最简状态{0}、{1}、{2，3}、{4}。
按次序重新命名为0、1、2、3，则得到最简DFA，以下列图所表示。第四章第四章第四章第四章第四章第四章第四章第四章0:S→·E
E→·aA
E→·bBLR(0)分析表为:(0)S→E (1)E→aА (2)E→bB (3)A→cА
(4)A→d (5)B→cB (6)B→d
输入串bccd$分析过程第四章(1)将文法G[S]拓广为文法G'[S']：
(0)S'→P
(1)P→m,r
(2)P→m,i
(3)P→r,r
(4)P→r,i
(5)P→r,m(0)S'→P (1)P→m,r (2)P→m,i
(3)P→r,r (4)P→r,i (5)P→r,m
输入串m,i$分析过程我们知道，LR(0)、SLR(1)和LR(1)分析表结构主要差异是结构算法。其区分以下：
(1)对LR(0)分析表来说，若项目A→α·属于Ik(状态)，则对任何终止符a(包含$)，置ACTION[k,a]为“用产生式A→α进行归约(A→α为第j个产生式)”，简记为“rj”。表现在ACTION子表中，则是每个归约状态所在行全部填满“rj”；而且，同一行“rj”其下标j相同，而不一样行“rj”其下标j是不一样。(2)对SLR(1)分析表来说，若项目A→α·属于Ik，则对任何输入符号a，仅当a∈FOLLOW(A)时置ACTION[k,a]为“用产生式A→α进行归约(A→α为第j个产生式)”，简记为“rj”。表现在ACTION子表中，则存在某个归约状态所在行并不全部填满rj，而且不一样行“rj”其下标j不一样。(3)对LR(1)来说，若项目[A→α·,a]属于Ik(状态)，则置ACTION[k,a]为“用产生式A→α进行归约”，简记为“rj”。LR(1)是在SLR(1)状态(项目集)基础上，经过状态分裂方法(即分裂成更多项目集)，使得LR分析器每个状态能够确切地指出当α后跟哪些终止符时才允许把α归约为A。比如，假定[A→α·,a]属于Ik(状态)，则置ACTION[k,a]栏目为rj(A→α为第j个产生式)；而[A→α·,b]属于Im(状态)，则一样置ACTION[m,b]栏目为rj。表现在ACTION子表中，则在不一样行(即不一样状态)里有相同rj存在。所以，图3-12(a)分析表为LR(1)分析表(在不一样行有相同r