结构方程模型市公开课一等奖省赛课获奖PPT课件.pptx

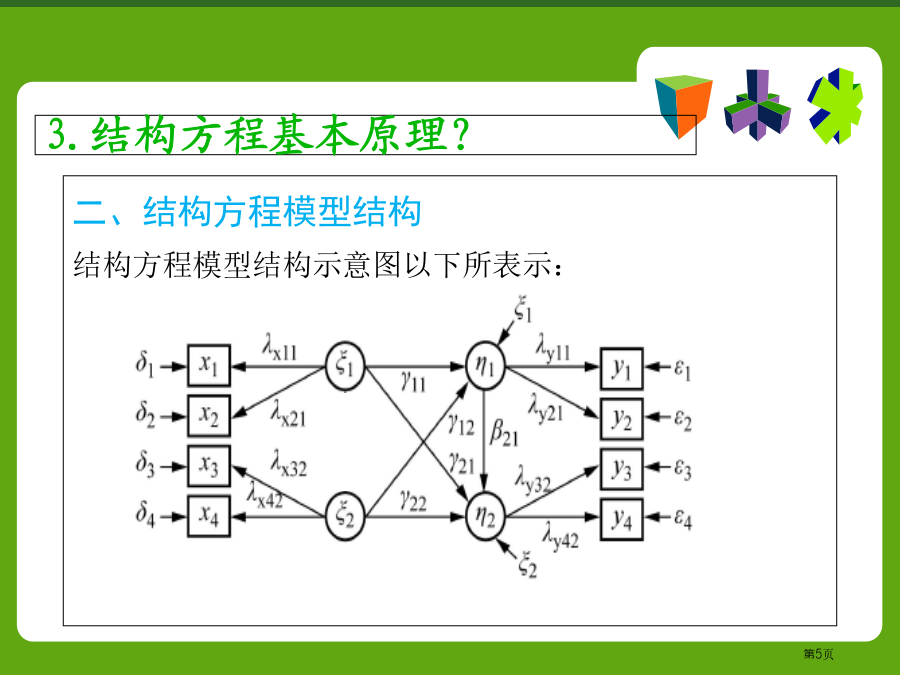
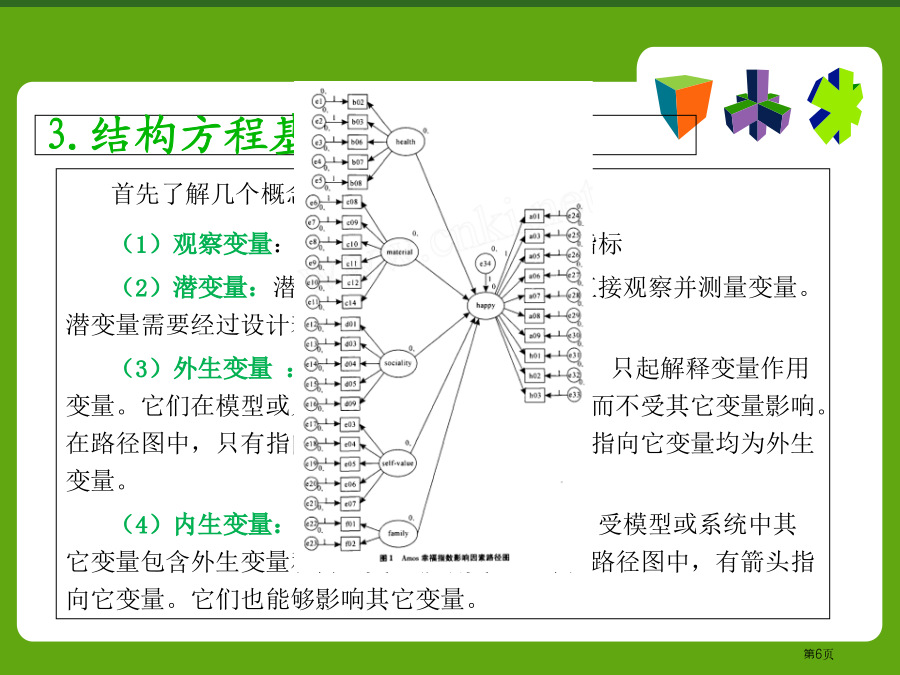
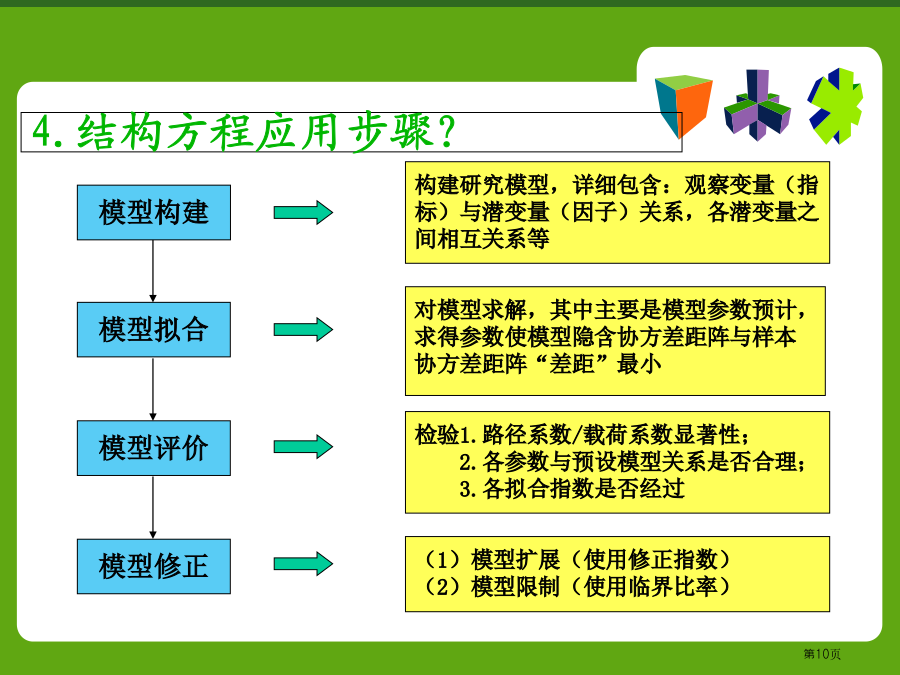
结构方程模型结构方程模型（StructuralEquationModel）是基于变量协方差矩阵来分析变量之间关系一个统计方法，所以也称为协方差结构分析。
它是综合利用多元回归分析、路径分析和验证型因子分析等方法而形成一个统计数据分析工具。其关键概念在20世纪70年代早期被提出，到80年代末期得以快速发展成为多元数据分析主要工具，广泛应用于心理学、经济学、社会学、行为科学等领域。

心理、教育、社会等领域有很多概念难以直接准确测量，称之为潜变量，如智力、学习动机、家庭社会经济地位等等。我们只能用一些外显指标去间接测量这些潜变量。另外，有时候需要处理多个原因和多个结果关系。这些都是传统统计方法不能很好处理问题
传统统计建模分析方法不能有效处理潜变量，而结构方程模型能同时处理潜变量和显变量（指标）。传统线性回归分析不允许有多个因变量存在测量误差，假设自变量是没有误差，结构方程模型则没有这些限制。

一、结构方程模型原理
结构方程模型基本思绪是:
首先，依据已经有理论和知识，经推理和假设形成一个关于一组变量之间相互关系模型；
然后，经过测查，取得一组观察变量(外显变量)数据和基于此数据而形成协方差矩阵，这种协方差矩阵称为样本矩阵。
最终，将构想假设模型与样本矩阵拟合程度进行检验，假如假设模型能拟合客观样本数据，说明模型成立；不然就要修正，假如修正之后依然不符合拟合指标要求，就要否定假设模型。

二、结构方程模型结构
结构方程模型结构示意图以下所表示：

首先了解几个概念：
（1）观察变量：可直接测量变量，通常是指标
（2）潜变量：潜变量亦称隐变量，是无法直接观察并测量变量。潜变量需要经过设计若干指标间接加以测量。
（3）外生变量：是指那些在模型或系统中，只起解释变量作用变量。它们在模型或系统中，只影响其它变量，而不受其它变量影响。在路径图中，只有指向其它变量箭头，没有箭头指向它变量均为外生变量。
（4）内生变量：是指那些在模型或系统中，受模型或系统中其它变量包含外生变量和内生变量影响变量，即在路径图中，有箭头指向它变量。它们也能够影响其它变量。

结构方程模型在形式上是反应隐变量和显变量关系一组方程，普通来讲由两类矩阵方程组成：

（1）测量方程（MeasurementEquation）

（2）结构方程（StructuralEquation）

（一）测量方程：
测量方程用来描述隐变量和显变量之间关系，能够写成以下通式：

其中：x——外生潜变量ξ可测变量组成向量；
y——内生潜变量η可测变量组成；
ξ——外生潜变量组成向量；
η——内生潜变量组成向量；
∧x——外生指标与外生变量之间关系，是外生指标在外生
潜变量上因子负荷矩阵；
∧y——内生指标与内生变量之间关系，是内生指标在内生
潜变量上因子负荷矩阵。
（二）结构方程：
结构方程用来描述隐变量之间关系关系，能够写成以下通式：

其中：ξ——外生潜变量组成向量；
η——内生潜变量组成向量；
B——内生隐变量间系数矩阵；
Γ——外生潜变量系数阵；
ζ——结构方程参差项，反应方程中未能被解释部分。

4.结构方程应用步骤？一、结构方程模型优点
总来说，与传统统计建模分析方法相比，结构方程模型主要有以下几个优点：
（1）允许回归方程自变量含有测量误差；
（2）能够同时处理多个因变量；
（3）能够在一个模型中同时处理原因测量和原因之
间结构；
(4)允许更具弹性模型设定。

二、结构方程模型不足
结构方程模型也存在一定不足：
（1）给定模型可能会产生无法解释结果；
（2）特定方法可能需要很大样本含量；
（3）需要满足多变量正态分布假设；
(4)极少用于预测应用；
（5）完全掌握结构方程需要基础知识、练习和努力；
（6）很多问题还没有很好答案和能够遵照指南。

谢谢观看！