内容提供者
26隐函数微分法省公开课一等奖全国示范课微课金奖PPT课件.pptx
2024-10-16
10金币
480KB
23页
lj****88
实名认证
内容提供者
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10
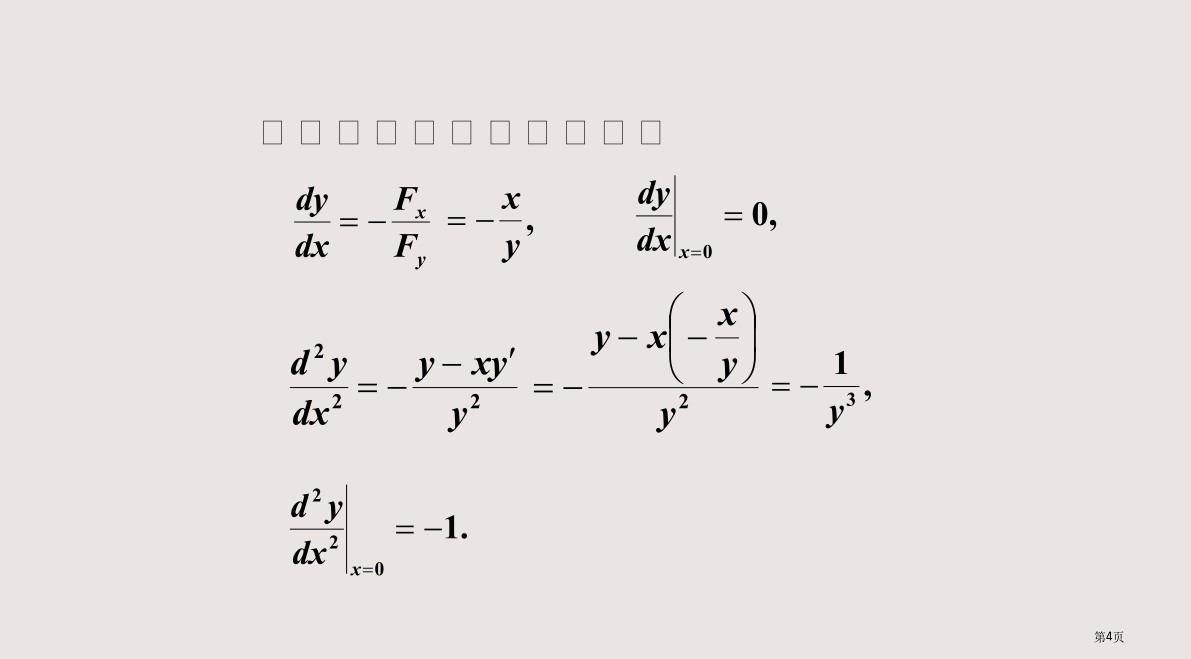
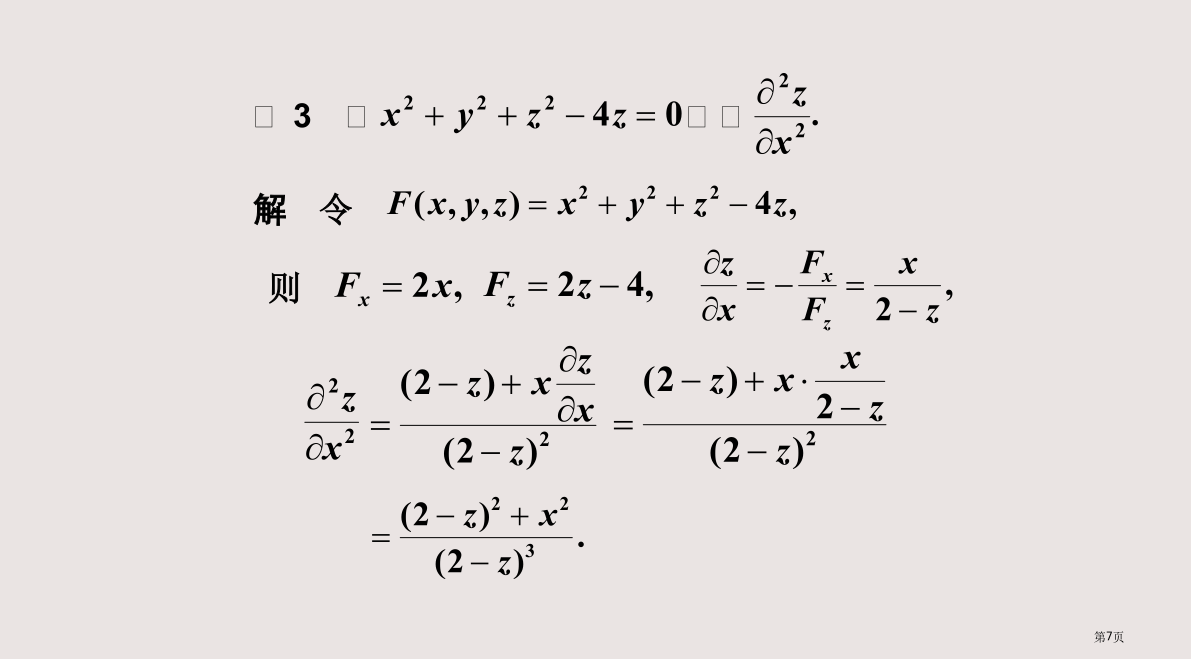
亲，该文档总共23页，到这已经超出免费预览范围，如果喜欢就直接下载吧～
相关资料
26隐函数微分法省公开课一等奖全国示范课微课金奖PPT课件.pptx
第六节隐函数微分法一、一个方程情形解解解例4设y=f(x,t),而t是由所确定函思绪：整理得整理得二、方程组情形解1将所给方程两边对求导，用一样方法得思索题思索题解答练习题练习题答案
2024-10-16
10
480KB
第6讲隐函数微分法省公开课金奖全国赛课一等奖微课获奖PPT课件.pptx
第六节隐函数微分法设设函数设利用点函数,将上面隐函数存在定理推广至普通n元函数情形.(隐函数存在定理)为了将一个方程确定隐函数求导方法推广至由方程组确定隐函数情形,我们首先要介绍雅可比行列式.雅可比行列式复合函数情形方程组中每个方程两边关于x求导：当同理可得在实际求解时,我们往往按照前面分析过程,对方程组中每一个方程两边关于某一个变量求导,然后解关于对应偏导数代数方程组.设注意!
2024-02-04
11
554KB
d925隐函数求导省公开课一等奖全国示范课微课金奖PPT课件.pptx
两边对x求导若F(x,y)二阶偏导数也都连续,例1.验证方程机动目录上页下页返回结束定理2.两边对x求偏导例2.设解法2公式法：二、方程组所确定隐函数组及其导数定理3.定理证实略.仅推导偏导数公式以下有隐函数组一样可得定理3′例4.设例5.设例6.设函数机动目录上页下页返回结束对方程两边求微分:内容小结提醒:解法2.利用全微分形式不变性同时求出各偏导数.补充题解:雅可比(1804–1851)
2024-10-16
10
795KB
142-隐函数的求导法则省公开课一等奖全国示范课微课金奖PPT课件.pptx
一、一元函数情形隐函数求导公式两边对x求导解函数一阶和二阶导数为解例3例4例5设例6设二、多元函数情形两边对x求偏导解思绪：整理得整理得补充：方程组情形1920解法1将所给方程两边对求导，用一样方法得（分以下几个情况）尤其地，一元隐函数求导法：思索题：因x=0时y=0,故2求椭圆3作业
2024-10-16
10
741KB
函数26幂函数与函数的图象变换省公开课一等奖全国示范课微课金奖PPT课件.pptx
重点难点重点：①幂函数定义、图象与性质．②函数图象三种基本变换规则．难点：①幂函数图象位置和形状改变与指数关系．②利用基本变换规则作函数图象普通幂函数图象形状特征及其分布．对于幂函数y＝xα(α∈R)，当α＝1时，y＝x图象是直线；当α＝0时，y＝x0＝1(x≠0)图象是直线(不包含(0,1)点)．其它普通情况图象以下表：3.性质：(1)当α>0时，幂函数图象都过点和点；且在第一象限都是函数；当0<α<1时曲线上凸；当α>1时，曲线下凸；α＝1时，为过(0,0)点和(1,1)点(2)当α<0时，幂函数图象
2024-10-16
10
854KB