
2017年《反比例函数》中考总复习-课件.ppt

lj****88









亲,该文档总共61页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

中考总复习课件《反比例函数》.ppt
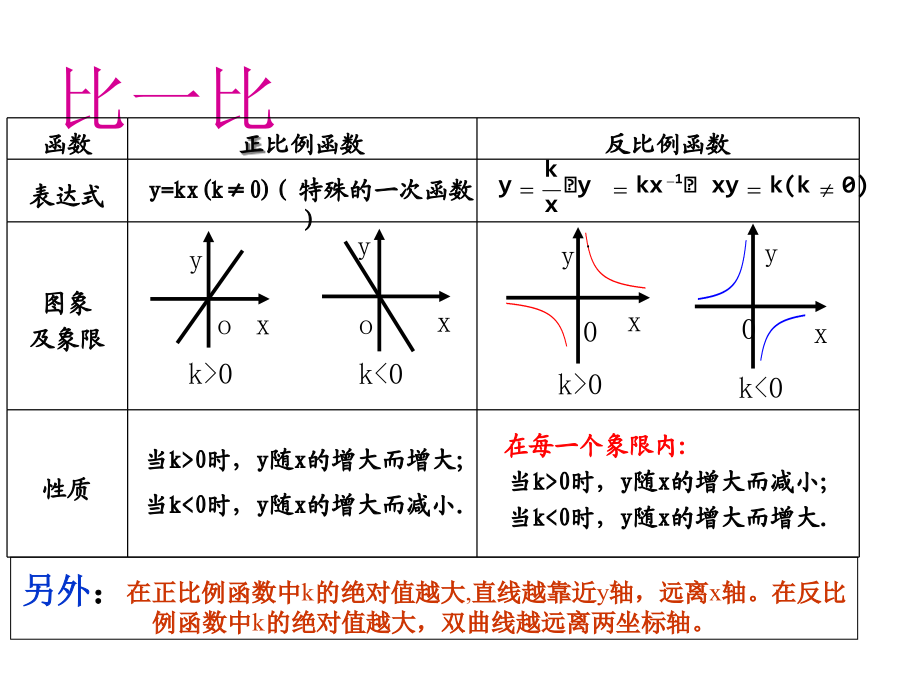
九年级总复习之反比例函数【反比例函数的定义】等价形式:(k≠0)K>0函数y=kx-k与在同一条直角坐标系中的图象可能是:P(m,n)P(m,n)确定反比例函数的解析式:实际问题

《反比例函数》中考总复习-课件.pptx
2023年《反百分比函数》中考总复习-课件1.什么叫反百分比函数?练习1:3.下列旳数表中分别给出了变量y与x之间旳相应关系,其中是反百分比函数关系旳是().函数比一比练习2:那么下列各点中一定也在此图象上旳点是()4.假如反百分比函数旳图象位于第二、四象限,那么m旳范围为.5、表达下面四个关系式旳图像有5、如图,函数和y=-kx+1(k≠0)在同一坐标系内旳图象大致是()7.考察函数旳图象,(1)当x=-2时,y=,(2)当x<-2时,y旳取值范围是;(3)当y≥-1时,x旳取值范围是.9、如图是一次函

2017年《反比例函数》中考总复习-课件.ppt
同学们努力吧,一切皆有可能﹗1.什么叫反比例函数?练习1:3.下列的数表中分别给出了变量y与x之间的对应关系,其中是反比例函数关系的是().函数比一比练习2:那么下列各点中一定也在此图象上的点是()4.如果反比例函数的图象位于第二、四象限,那么m的范围为.5、表示下面四个关系式的图像有5、如图,函数和y=-kx+1(k≠0)在同一坐标系内的图象大致是()7.考察函数的图象,(1)当x=-2时,y=,(2)当x<-2时,y的取值范围是;(3)当y≥-1时,x的取值范围是.9、如图是一次函数y1=kx+b和反

2017年《反比例函数》中考总复习-课件.ppt
同学们努力吧,一切皆有可能﹗1.什么叫反比例函数?练习1:3.下列的数表中分别给出了变量y与x之间的对应关系,其中是反比例函数关系的是().函数比一比练习2:那么下列各点中一定也在此图象上的点是()4.如果反比例函数的图象位于第二、四象限,那么m的范围为.5、表示下面四个关系式的图像有5、如图,函数和y=-kx+1(k≠0)在同一坐标系内的图象大致是()7.考察函数的图象,(1)当x=-2时,y=,(2)当x<-2时,y的取值范围是;(3)当y≥-1时,x的取值范围是.9、如图是一次函数y1=kx+b和反

《反比例函数》中考总复习.docx
《反比例函数》中考总复习练习设计中伙铺镇中学昌先华一、课堂练习设计:(一)反比例函数的意义:1、下列函数是反比例函数的是_____________.xy0(-3,1)(1)y=,(2)y=3x,(3),(4),(5)(k为常数,k≠0),(6).2、已知函数是反比例函数,则m=_____.(第4题图)3、函数y=,当a=___时,是正比例;当a=___时,是反比例函数。4、用待定系数法求反比例函数的解析式。根据图形写出函数的解析式:_______________.(二)反比例函数的图像和性质:1、已知函数
