
(中小学教案)(第8课时)§1.3 基本算法语句——循环语句.doc

xf****65



在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

(中小学教案)(第8课时)§1.3 基本算法语句——循环语句.doc
东台市富安中学高二数学教学案东台市富安中学高二数学教学案普通高中课程标准实验教科书—数学必修三[苏教版]普通高中课程标准实验教科书—数学必修三[苏教版](第8课时)§1.3基本算法语句——循环语句教学目标:1.掌握两种循环语句的一般形式,进一步体会算法的基本思想.2.能够熟练地运用两种循环语句.教学重点:两种循环语句的形式和特点教学过程:一、问题情境猴子第一天摘下若干个桃子,当即吃了一半,觉得还不过瘾,又多吃了一个.第二天将剩下的桃子吃掉一半,又多吃了一个,以后每天都吃前一天剩下的一半加一个.到第十天想吃

(中小学教案)§1.3 基本算法语句——循环语句.doc
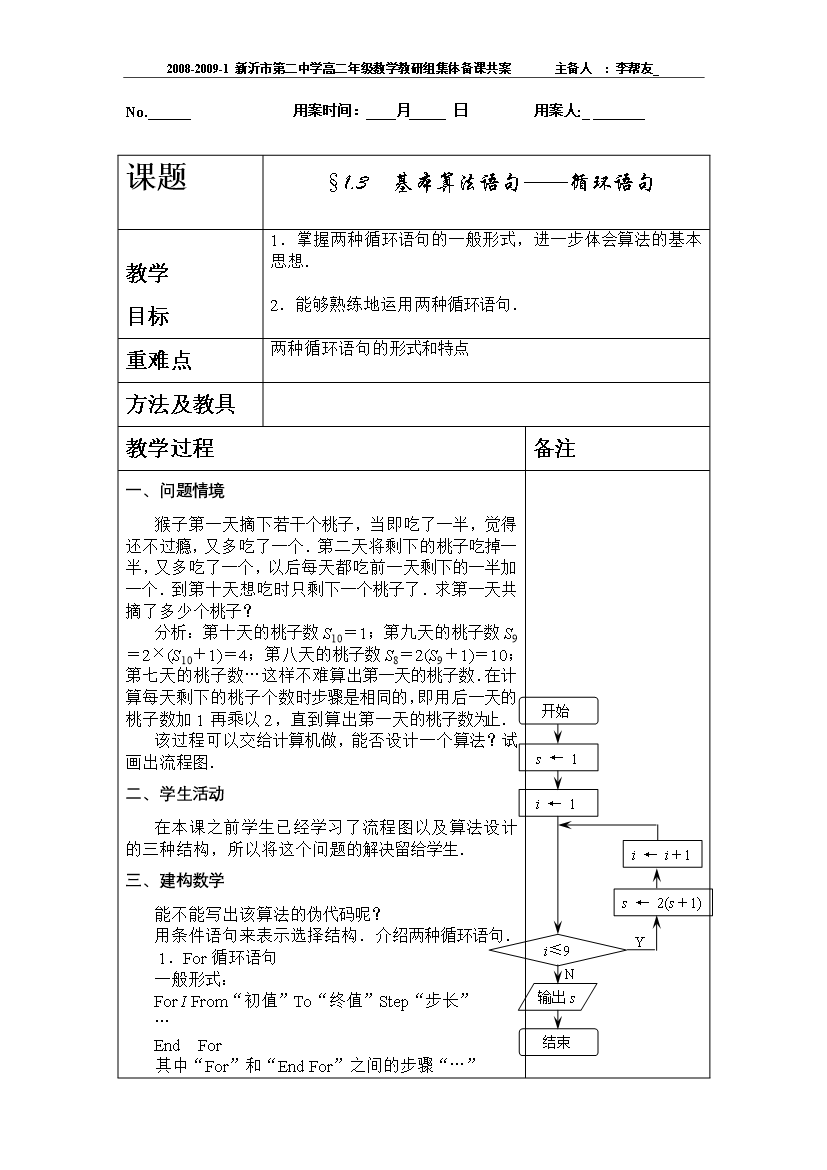
2008-2009-1新沂市第二中学高二年级数学教研组集体备课共案主备人:李帮友_No.______用案时间:____月_____日用案人:________课题§1.3基本算法语句——循环语句教学目标1.掌握两种循环语句的一般形式,进一步体会算法的基本思想.2.能够熟练地运用两种循环语句.重难点两种循环语句的形式和特点方法及教具教学过程备注一、问题情境猴子第一天摘下若干个桃子,当即吃了一半,觉得还不过瘾,又多吃了一个.第二天将剩下的桃子吃掉一半,又多吃了一个,以后每天都吃前一天剩下的一半加一个.到第十天想
§1.3 基本算法语句——循环语句.doc
2008-2009-1新沂市第二中学高二年级数学教研组集体备课共案主备人:李帮友_No.______用案时间:____月_____日用案人:________课题§1.3基本算法语句——循环语句教学目标1.掌握两种循环语句的一般形式进一步体会算法的基本思想.2.能够熟练地运用两种循环语句.重难点两种循环语句的形式和特点方法及教具教学过程备注一、问题情境猴子第一天摘下若干个桃子当即吃了一半觉得还不过瘾又多吃了一个.第二天将剩下的桃子

(中小学教案)(第7课时)§1.3 基本算法语句——条件语句.doc
东台市富安中学高二数学教学案东台市富安中学高二数学教学案普通高中课程标准实验教科书—数学必修三[苏教版]普通高中课程标准实验教科书—数学必修三[苏教版](第7课时)§1.3基本算法语句——条件语句教学目标:(1)正确理解条件语句的步骤、结构及功能,并掌握其结构;(2)能正确地使用条件语句表示选择结构.教学重点:条件语句的步骤、结构及功能.教学难点:使用条件语句表示选择结构.教学过程:一、问题情境1.问题1:某居民区的物业管理部门每月按以下方法收取卫生费:3人和3人以下的住户,每户收取5元;超过3人的住户,

(中小学教案)(第6课时)§1.3 基本算法语句.doc
东台市富安中学高二数学教学案东台市富安中学高二数学教学案普通高中课程标准实验教科书—数学必修三[苏教版]普通高中课程标准实验教科书—数学必修三[苏教版](第6课时)§1.3基本算法语句——赋值、输入、输出语句教学目标:(1)正确理解赋值语句、输入语句、输出语句的结构;(2)让学生充分地感知、体验应用计算机解决数学问题的方法;(3)通过实例,使学生理解3种基本的算法语句(输入语句、输出语句和赋值语句)的表示方法、结构和用法,能用这三种基本的算法语句表示算法,进一步体会算法的基本思想.教学重点:正确理解输入语
