流体应变率张量学习教案.pptx

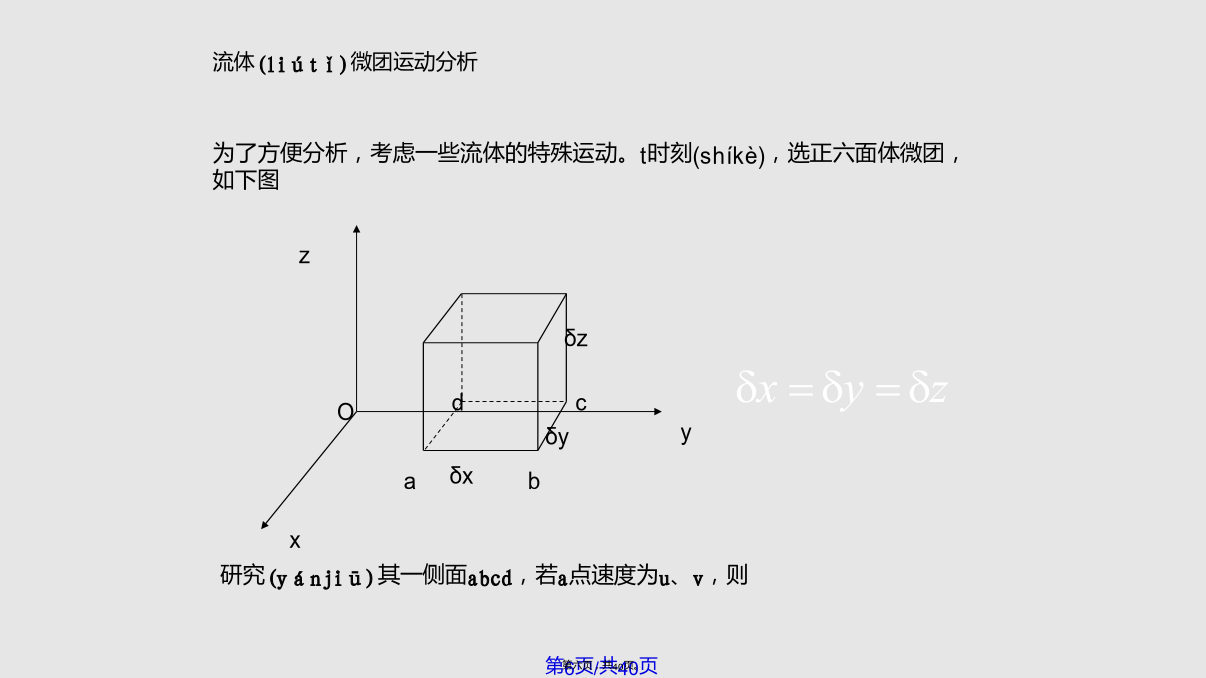
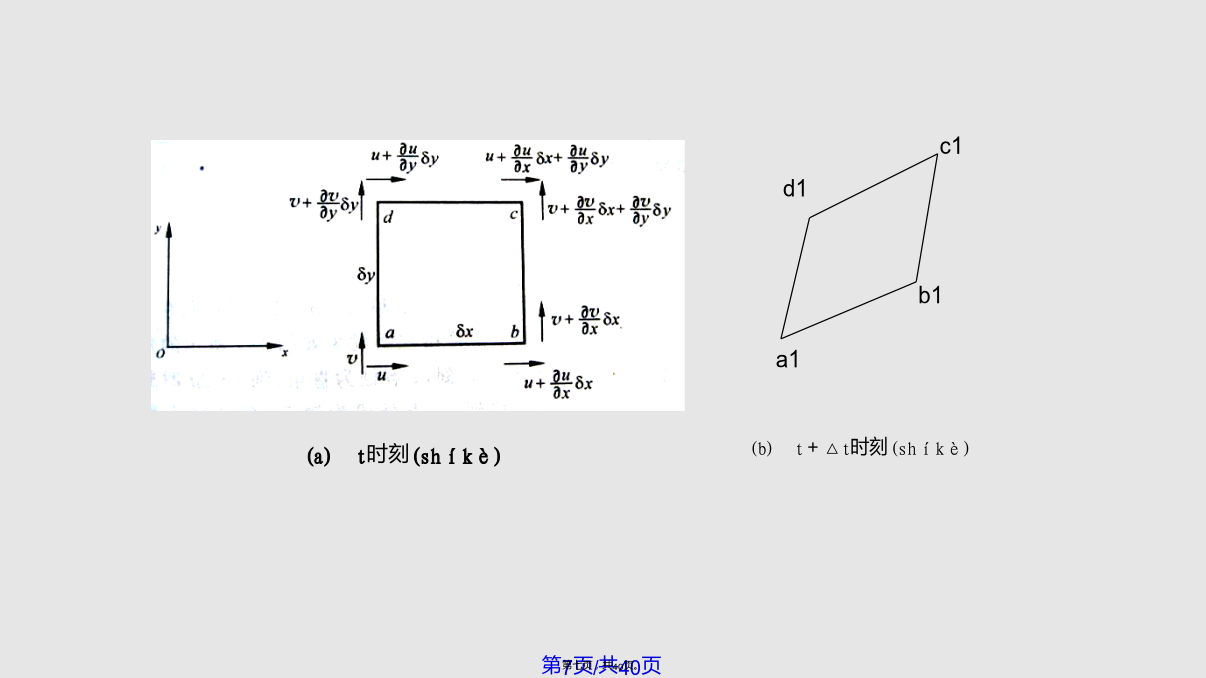
亥姆霍兹速度分解(fēnjiě)定理写成分量(fènliàng)形式：对称(duìchèn)或而流体(liútǐ)微团运动分析(a)t时刻(shíkè)1.线变形分析（相对(xiāngduì)伸长速度）各边的相对伸长，将引起流体微团体(tuántǐ)积膨胀，在△t时刻后，正方形体积，已变为2.角变形(biànxíng)分析(角变形(biànxíng)速度)3.流体微团旋转(xuánzhuǎn)分析（旋转(xuánzhuǎn)角速度）存在不在质点(zhìdiǎn)连线方向的速度梯
度是产生旋转和角变形的原因各分量都有明确的物理意义，其中三个代表线段的相对伸长率（速度），三个代表角变形率（速度），三个代表流体(liútǐ)本身的自转角速度，另外速度散度代表流体(liútǐ)体积相对膨胀率。例：平面流场ux=ky，uy=0（k为大于0的常数），分析(fēnxī)流场运动特征例：平面流场ux=－ky，uy=kx（k为大于0的常数(chángshù)），分析流场运动特征1.有旋流动(liúdòng)例：速度场u=ay（a为常数），v=0，流线是平行于x轴的直线(zhíxiàn)，此流动是有旋流动还是无旋流动？例：速度场ur=0，uθ=b/r（b为常数(chángshù)），流线是以原点为中心的同心圆，此流场是有旋流动还是无旋流动？流体运动(yùndòng)的分类2.粘性流动(liúdòng)和无粘性流动(liúdòng)
这是从流体运动和剪切变形的角度来考虑的分类方法；
静止的流体不呈现粘性；
对于运动流体，在实际应用过程中常通过流体中粘性切应力与其它力（主要是流动(liúdòng)惯性力）在大小量级上的比较来考虑粘性效应。把忽略粘性效应的流动(liúdòng)称为无粘性流体流动(liúdòng)，简单地令
无粘性流动(liúdòng)在流体力学理论中占有重要地位。3.定常流动和非定常流动
这是从物理量对时间t的依赖关系的角度来考虑的分类方法；
流场中速度等物理量不随时间变化的流动称为定常流动，数学上简单(jiǎndān)地表示为
定常是相对的，不定常是绝对的，对于随时间变化缓慢的流动，如大容器的小孔出流等
定常流动的研究和处理要比非定常流动要容易得多。4.一维流动、二维流动和三维流动
这是从物理量对空间坐标（x，y，z）的依赖关系的角度来考虑的分类方法；
如果流动中，所有物理量只与一个空间变量有关，则称此流动为一维流动，依次类推。
实际工程中很难找到真正一维流动，在微元流管中的流动是最接近一维的流动。有限截面管中流动，有时为了计算(jìsuàn)方便，仅考虑按截面平均后的量，此时可看作一维流动，或准一维流动。
二维流动包括平面流动和轴对称流动；
三维流动是一种空间流动。5.有旋流动和无旋流动
这是从流体微团运动分析的角度来考虑的分类方法；
如果在整个流场中流体微团的旋转角速度为0，则称此流动为无旋流动。在流速分布已知的情况下可根据速度的旋度是否为0加以判断；
一般而言，粘性流体的流动总是有旋的，无粘性流体的流动有可能有旋也可能无旋。例如当流体既忽略粘性又忽略重力时，从静止启动的流动就是无旋的，大气中的气旋和海洋环流等都是典型的有旋运动。
除了(chúle)这些分类方法，还有粘性流体运动中的层流、湍流，可压缩流动还有亚声速和超声速之分等。1.8流体(liútǐ)中的作用力与应力张量若已知f，则作用(zuòyòng)在有限体积内流体上的总体积力为：表面(biǎomiàn)力与应力流场中任一点的应力(yìnglì)状态——应力(yìnglì)张量受力分析(fēnxī)
作用在四面体上的力有表面力和质量力（包括惯性力），表面力与面积成正比，为二阶小量；质量力与体积成正比为三阶小量，当四面体缩小为一点，忽略三阶小量，则表面力的合力将等于0，则有写成矩阵(jǔzhèn)形式表明了表面应力与外法向单位(dānwèi)矢量的关系静止流体与运动(yùndòng)的无粘性流体中的应力张量上式说明了流体中静压力的两个重要特性：
流场中一点静压强（压力）大小各向等值，即与过同一点作用面的方位无关，因此p是个标量物理量，它只是该点的空间坐标的函数;
2.一点上的静压（压力）总是(zǒnɡshì)垂直指向过该点的作用面例题：流体(liútǐ)内某处的应力张量为该应力矢量(shǐliàng)在平面x＋3y＋z＝1外侧法向分量为复习(fùxí)思考题6.什么是理想流体？为什么要引进理想流体这一概念？理想流体有无能量损失？
7.什么情况下要考虑流体的压缩性？为什么液体(yètǐ)通常可以看成不可压缩流体，气体在速度小于100m/s时也可以看做是不可压缩流体？
8.描述流体运动有哪两种方法？两种方法有什么不同？两种方法是如何转换的？
9.什么是流线与迹线，流线有什么性质