
材料扩散学习教案.pptx

快乐****蜜蜂








亲,该文档总共71页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

材料扩散学习教案.pptx
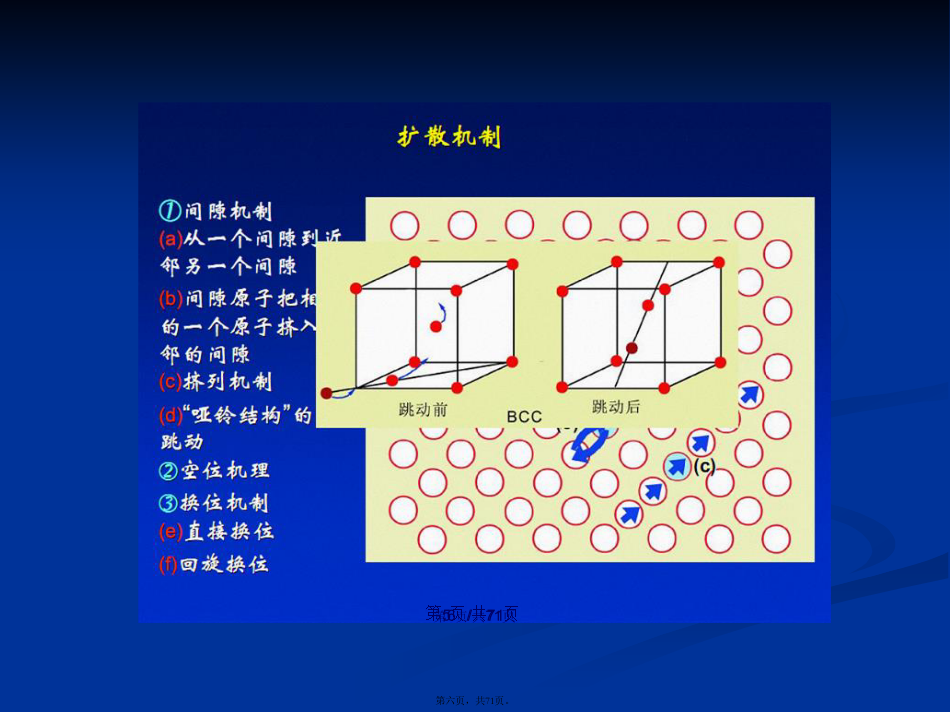
会计学(////空位(kōnɡwèi)扩散对于纯金属或形成置换式因溶体合金,原于都是处于正常的晶格结点位置实现空位机制的条件:扩散原子的近邻应当有空位,同时空位周围的原子还必须具有超过(chāoguò)能垒的自由能//溶质原子沿x方向在垂直于纸面两平行原子面之间的扩散情况。经过一段时间后,两处的溶质原子浓度分别为c1和c2,且不再随时间变化,这种扩散条件称为稳态扩散。一个不会发生反应作用的气体通过金属薄膜时就会进行这种扩散,例如氢气扩散通过铝的薄膜时,如果氢气在一侧处于高压,而在另一侧处于低压(dīyā)

材料物理材料的固态扩散PPT学习教案.pptx
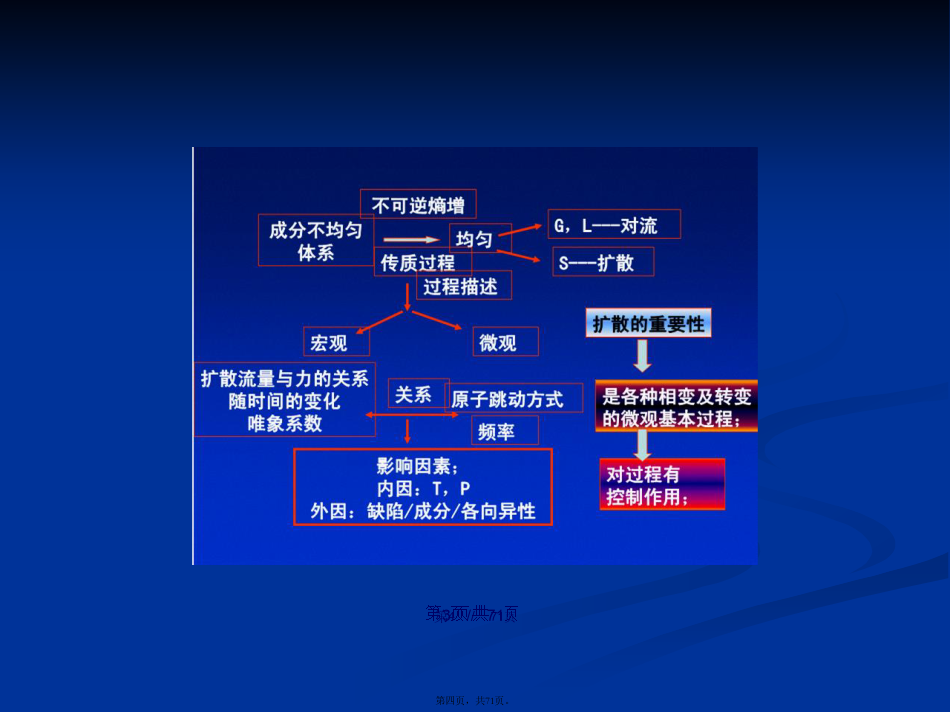
会计学当固体中有不同种粒子同时存在(cúnzài)时,粒子由高浓度处向浓度低的处方迁移,这种现象称为扩散。同种粒子也可以在固体中迁移,称为自扩散,如Cu、Fe原子分别在其晶体中的迁移。扩散现象首先是在研究铁—铂合金时由法拉第发现的,并在合金方面得到了迅速的应用和发展。在硅酸盐材料的生产和研究中,扩散对于固相反应、烧结、析晶、分相以及熔化等动力学过程有十分重要的意义,并且对材料的性质有重大影响。扩散:物质中原子或分子迁移的现象。扩散的重要性:铸件的均匀化,许多固态相变过程,表面合金化,冷变形金属的回复,再结

材料物理材料的固态扩散学习教案.pptx
会计学当固体中有不同种粒子同时存在时,粒子由高浓度处向浓度低的处方迁移,这种现象(xiànxiàng)称为扩散。同种粒子也可以在固体中迁移,称为自扩散,如Cu、Fe原子分别在其晶体中的迁移。扩散现象(xiànxiàng)首先是在研究铁—铂合金时由法拉第发现的,并在合金方面得到了迅速的应用和发展。在硅酸盐材料的生产和研究中,扩散对于固相反应、烧结、析晶、分相以及熔化等动力学过程有十分重要的意义,并且对材料的性质有重大影响。扩散:物质中原子或分子迁移的现象。扩散的重要性:铸件的均匀化,许多(xǔduō)固态相

材料科学基础扩散学习教案.pptx
会计学固体(gùtǐ)中的扩散扩散(diffusion):由于物质中原子(或者其他微观粒子)的微观热运动(yùndòng)所引起的宏观迁移现象。气体(qìtǐ)在固体中的原子和分子(fēnzǐ)是在不停地运动研究扩散(kuòsàn)可以从两个角度:唯象(PhenomenologicalApproach)原子结构(Atomisticapproach)材料制备、加工和服役的许多过程(guòchéng)与扩散有关。如:相变氧化蠕变烧结表面处理等固体(gùtǐ)中的扩散稳态扩散(steady-statediffu

材物扩散学习教案.pptx
会计学几个(jǐɡè)实例第一节引言第一节概述(ɡàishù)1.1扩散能够(nénggòu)进行的原因:扩散推动力当不存在外场时,晶体中粒子的迁移完全是由于热振动引起的。只有在外场作用下,这种粒子的迁移才能形成定向的扩散流。也就是说,形成定向扩散流必需要有推动力,这种推动力通常是由浓度梯度提供的。Q235钢板(gāngbǎn)偏析但应指出,在更普遍情况下,扩散推动力应是系统的化学位梯度.物质从高化学位流向低化学位是更普遍的规律,一切影响扩散的外场——浓度场、电场(diànchǎng)、磁场、应力场等,都
