数值分析曲线拟合与线性最小二乘问题学习教案.pptx

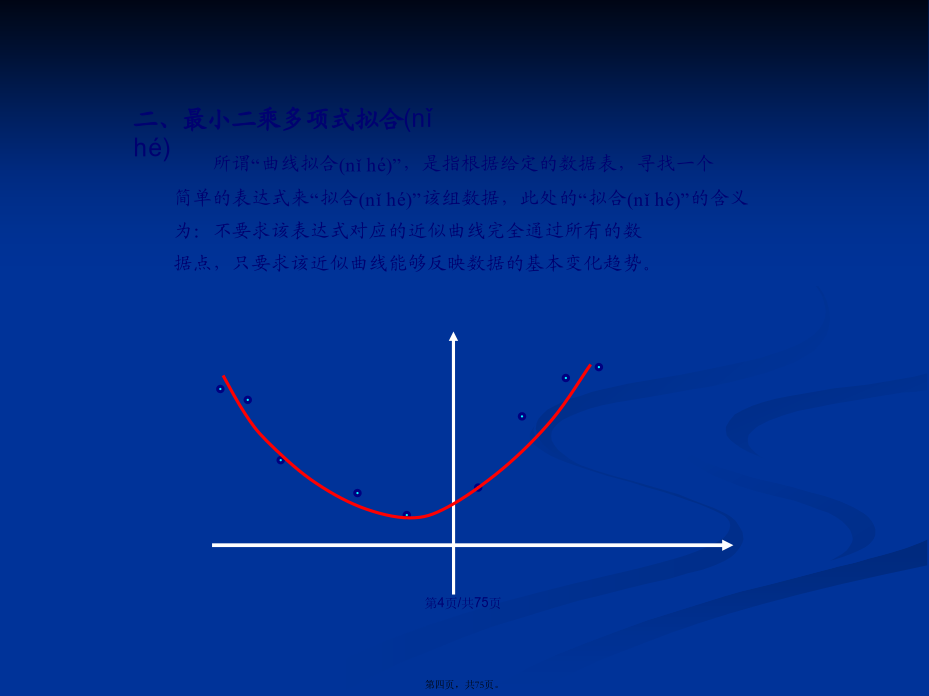
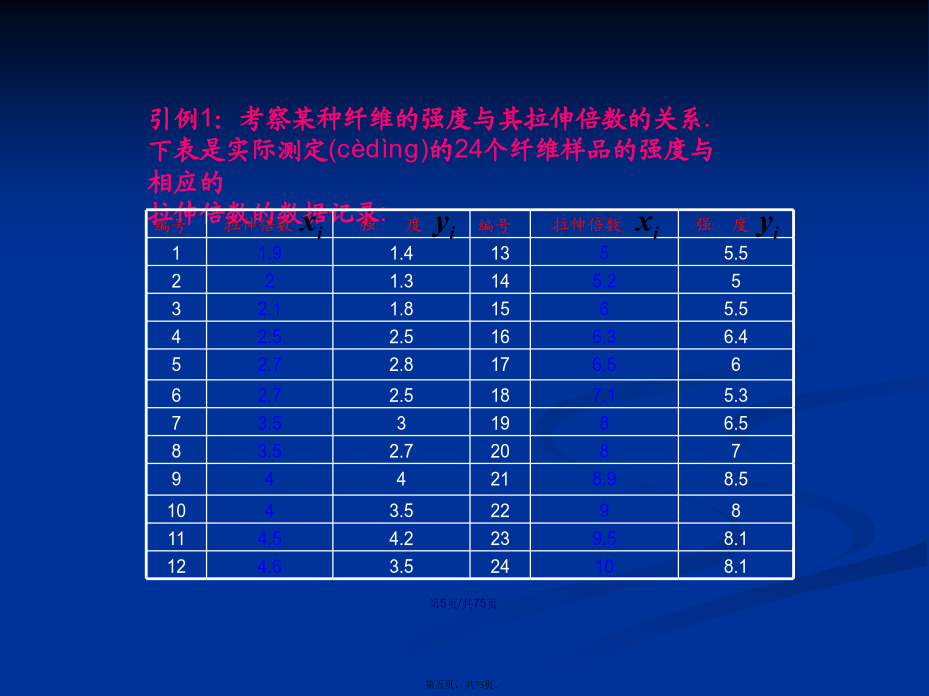
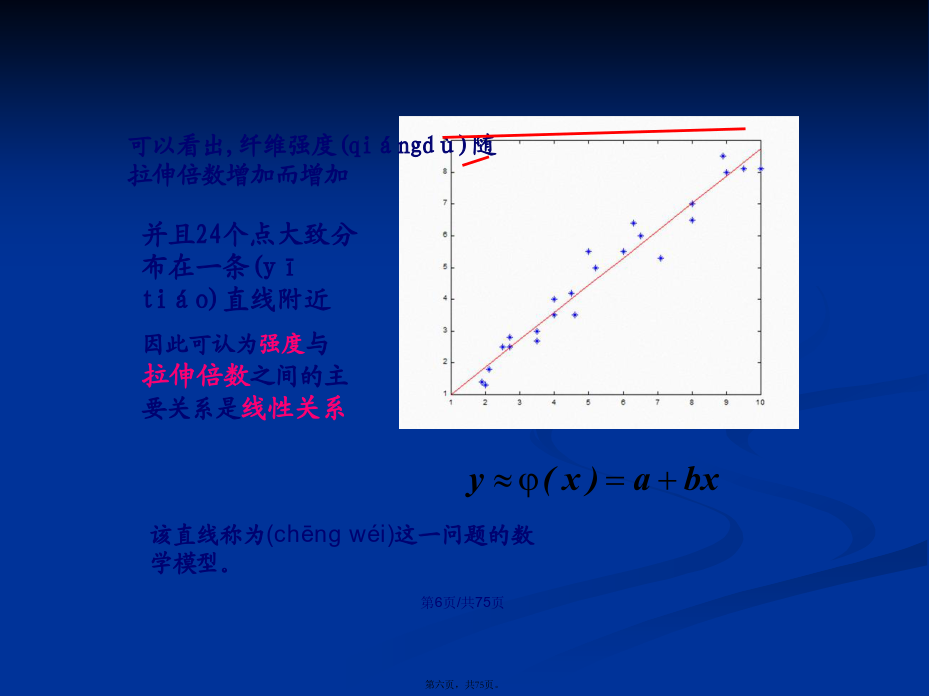
会计学称为(chēnɡwéi)
残向量所谓“曲线拟合(nǐhé)”，是指根据给定的数据表，寻找一个
简单的表达式来“拟合(nǐhé)”该组数据，此处的“拟合(nǐhé)”的含义
为：不要求该表达式对应的近似曲线完全通过所有的数
据点，只要求该近似曲线能够反映数据的基本变化趋势。引例1：考察某种纤维的强度与其拉伸倍数的关系.
下表是实际测定(cèdìng)的24个纤维样品的强度与相应的
拉伸倍数的数据记录:可以看出,纤维强度(qiángdù)随
拉伸倍数增加而增加怎样确定a,b,使得直线能较好地反映(fǎnyìng)所给数据的基
本“变化趋势”?这种求线性函数y=a+bx的过程称为(chēnɡwéi)线性拟合。一般地，设的近似函数为非线性拟合(nǐhé)又如：若非线性函数取为三、最小二乘问题(wèntí)解的存在性、唯一性不妨假设的前列线性无关(满秩分解(fēnjiě))二乘解的充要条件是为方程组的解。必要性推论7.1.2若，则方程组例1：求下列方程组的最小二乘解解：写出法方程组§2广义(guǎngyì)逆矩阵与最小二乘解
/*GeneralizedInverseMatrixandLeastSquaresSolution*/设 ，则方程组（P1–P4)有唯一解，且解为。若，则Penrose方程变为二、广义(guǎngyì)逆的分类§3正交化方法(fāngfǎ)/*OrthogonalizationMethod*/Gram-Schmidt正交化方法(fāngfǎ)：Step1令二、改进(gǎijìn)的Gram-Schmidt正交化方法：则（*）式的第2式至第n式化为记记经过r步后得到MGS算法(suànfǎ)：例3：用MGS方法求下列

矩阵的正交分解Step2上述情况下极小(jíxiǎo)最小二乘解的求法：例4：用MGS方法求下列

方程组的极小最小二乘解.三、正交分解(fēnjiě)和线性方程组的最小二乘解令设，且，且其中为方程组的唯一解；证明(zhèngmíng)：一般(yībān)情况下极小最小二乘解的求法：四、Householder变换(biànhuàn)与Givens变换(biànhuàn)设，且，则存在H-矩阵，H-矩阵(jǔzhèn)的计算H-矩阵在正交分解(fēnjiě)中的应用具体步骤：经过(jīngguò)r步后得到：例5：用Householder变换求

下列方程组的极小最小二乘解Step2/方程组的极小(jíxiǎo)最小二乘解的求法同例42、Givens变换(biànhuàn)（平面旋转变换(biànhuàn)）:令例6：用Givens旋转变换求

下列方程组的极小最小二乘解/Step2Step3/Step4Step5感谢您的观看(guānkàn)！