预览加载中，请您耐心等待几秒...

2.3.1__离散型随机变量的均值.pptx

预览
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10

亲，该文档总共18页，到这已经超出免费预览范围，如果喜欢就直接下载吧～

下载提示 文本预览

如果您无法下载资料，请参考说明：

1、部分资料下载需要金币，请确保您的账户上有足够的金币

2、已购买过的文档，再次下载不重复扣费

3、资料包下载后请先用软件解压，在使用对应软件打开

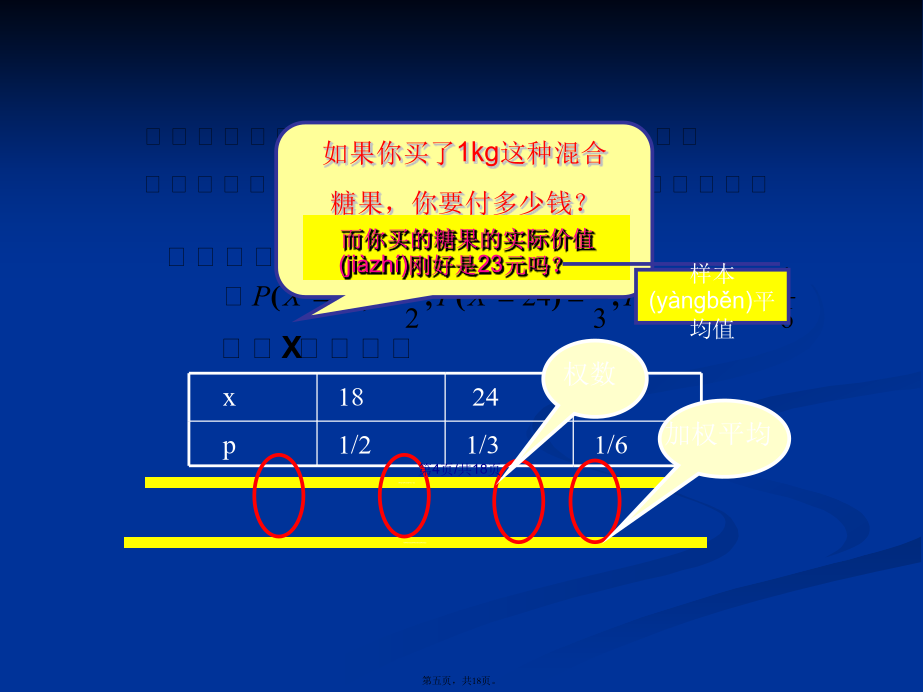
会计学如果你期中考试各门成绩为： 90、80、77、68、85、91 那你的平均(píngjūn)成绩是多少？引入：某商场为满足市场需求要将单价分别为18元/kg，24元/kg，36元/kg的3种糖果按3：2：1的比例混合销售(xiāoshòu)，其中混合糖果中每一颗糖果的质量都相等，如何对混合糖果定价才合理？x思考(sīkǎo)下面的问题:一般地： 对任一射手,若已知他的所得环数的分布列，即已 知则可以预计他任意n次射击的 平均环数是记为 它反映(fǎnyìng)了离散型随机变量取值的平均水平.例题(lìtí)1例2、所以，的分布列为1、随机变量(suíjībiànliànɡ)ξ的分布列是例3:在篮球比赛中，如果某运动员罚球命中的概率为0.7，那么他罚球一次得分设为X，X的均值(jūnzhí)是多少？3.篮球运动员在比赛中每次罚球命中得1分，罚不中得0分．已知某运动员罚球命中的概率(gàilǜ)为0.7，则他罚球1次的得分ξ的期望为．∴Eξ=0×Cn0p0qn+1×Cn1p1qn-1+2×Cn2p2qn-2+ …+k×Cnkpkqn-k+…+n×Cnnpnq0不一定,其含义是在多次类似的测试中,他的平均成绩(chéngjì)大约是90分练习：一个袋子里装有大小相同的3个红球和2个黄球，从中有放回地取5次，则取到红球次数(cìshù)的数学期望是.1、离散型随机变量均值(jūnzhí)的定义