管理运筹学单纯形法的灵敏分析与对偶对偶问题课程.pptx

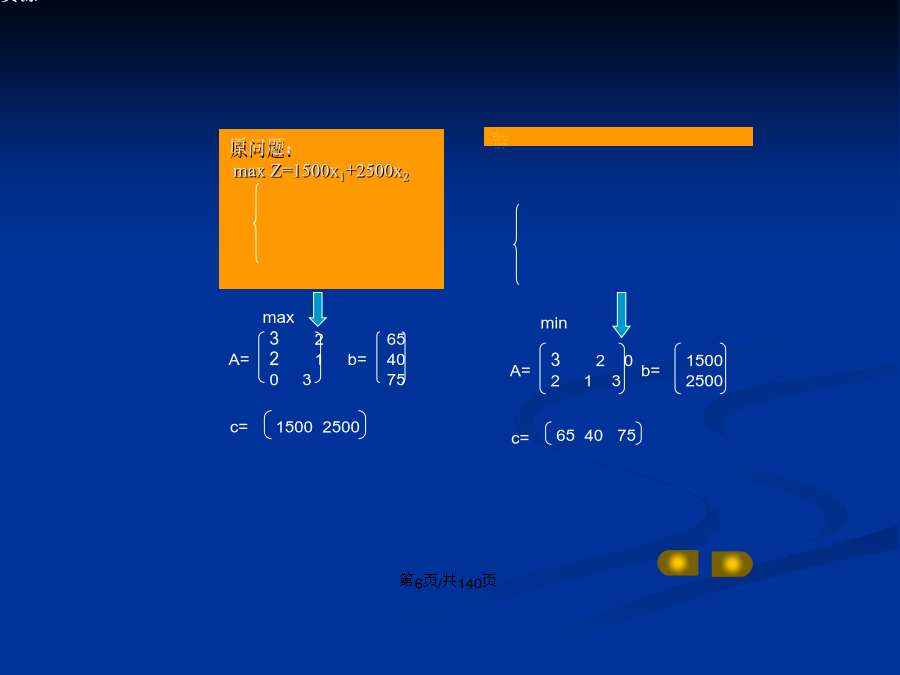
会计学Cj第六章单纯形法的灵敏度分析与对偶§1单纯形表的灵敏度分析(重点.难点.掌握)
§2线性规划的对偶问题(重点.理解.掌握)
§3对偶规划的基本性质(重点.应用)
§4对偶单纯形法(难点.掌握---前面已讲)
§2线性规划的对偶问题考虑：
1、定价不能太高？
2、定价不能太低？原问题：
maxZ=1500x1+2500x2
s.t.3x1+2x265A资源
2x1+x240B资源
3x275C资源
x1,x20对偶问题MinW=bTYs.t.ATY≥CT
Y≥0对偶关系表由表可以看出：

从行看是原问题（Ⅰ），从列看是对偶问题（Ⅱ），两个问题的变量系数矩阵互为转置矩阵。
原问题（Ⅰ）的常数项是对偶问题（Ⅱ）的目标系数，反之，原问题（Ⅰ）的目标系数是对偶问题（Ⅱ）的常数项。
原问题（Ⅰ）有n个决策变量，对偶问题（Ⅱ）有n个约束方程；原问题有m个约束方程，对偶问题就有m个决策变量。
原问题的约束是“≤”型，对偶问题的约束是“≥”型。
原问题的目标函数是求极大，对偶问题的目标是求极小。maxZ＝5x1+4x22、非对称型对偶问题
表对偶变换的规则例3：对称形式线形规划问题为:最优基maxZ=2x1+x2
5x2≤15
s.t.6x1+2x2≤24
x1+x2≤5
x1,x2≥0minZ=2x1+3x2+x3
x1+4x2+2x3≥8
S.t.3x1+2x2≥6
x1,x2,x3≥0

CjmaxZ=50x1+100x2
x1+x2≤300
s.t.2x1+x2≤400
x2≤250
x1,x2≥0已知最优基的基变量为x1，x4，x2，请直接写出该线性规划问题的最终单纯形表。并给出其对偶问题的最优解对应初始单纯表中的单位矩阵I，迭代后的单纯形表中为B-1
初始单纯表中的基变量Xs=b，迭代后的单纯形表中为XB=B-1b
初始单纯表中的约束系数矩阵为：
[A,I]=[B,N,I]
迭代后的单纯形表中约束系数矩阵为：
[B-1A,B-1I]=[B-1B,B-1N,B-1I]=[I,B-1N,B-1]
若初始矩阵中变量xj的系数向量为Pj，迭代后为Pj`，则有：
Pj`=B-1Pj当B为最优基时，迭代后的单纯表中检验数：CN-CBB-1N≤0
-CBB-1≤0
因XB的检验数可写为：CB-CBB-1B
故可重写为：C-CBB-1A≤0
-CBB-1≤0
CBB-1称为单纯形乘子。若令YT=CBB-1则：C-YTA≤0ATY≥C
所以：ATY≥CT
Y≥0可见检验数的相反数恰好是其对偶问题的一个可行解，将这个解代入对偶问题的目标函数，有：maxZ=2x1+x2
5x2≤15
s.t.6x1+2x2≤24
x1+x2≤5
x1,x2≥0例6、利用原问题的最优单纯形表求解对偶问题的最优解Cj为了便于讨论，下面不妨总是假设:î定理2（弱对偶性定理）
对偶问题(min)的任何可行解Y0，其目标函数值总是不小于原问题(max)任何可行解X0的目标函数值。例7、应用弱对偶定理，证明下列线性规划问题的最大值不超过1.弱对偶定理推论推论2如果原max(min)问题为无界解，则其对偶min(max)问题无可行解(反之不然)推论3原问题(max)的任何可行解目标函数值是其对偶问题(min)目标函数值的下界；原问题(min)的任何可行解目标函数值是其对偶问题(max)目标函数值的上界
推论4如果原问题max(min)有可行解，其对偶问题min(max)无可行解，则原问题为无界解例8、应用对偶理论证明下列线性规划问题目标函数值无界.定理3主对偶定理(强对偶性定理)
如果原问题和对偶问题都有可行解，则它们都有最优解，且它们的最优解所对应的目标函数值相等。
定理4互补松弛定理
定理设X0,Y0分别是原问题和对偶问题的可行解，U0为原问题的松弛变量的值、V0为对偶问题剩余变量的值。X0,Y0分别是原问题和对偶问题最优解的充分必要条件是Y0U0=V0X0=0
例9、考虑下列原始线性规划（2）由题知原问题的最优解为例10：利用互补松弛定理/原问题检验数与对偶问题的解的总结
在主对偶定理(强对偶性)的证明中我们有：对偶(min型))变量的最优解等于原问题松弛变量的机会成本，或者说原问题松弛变量检验数的绝对值
容易证明，对偶问题最优解的剩余变量解值等于原问题对应变量的检验数的绝对值
由于原问题和对偶问题是相互对偶的，因此对偶问题的检验数与原问题的解也有类似上述关系。
更一般地讲，不管原问题是否标准，在最优解的单纯型表中，都有原问题虚变量(松弛或剩余)的检验数对应其对偶问题实变量(对偶变量)的最优解，原问题实变量(决策变量)的检验数对应其对偶问题虚变量(松弛或剩余变量)的最优解。因此，原问题或对偶问题只需求解其中之一就可以了。§4对偶单纯形法二、对偶单纯形法的计算步