角动量角动量守恒课程.pptx

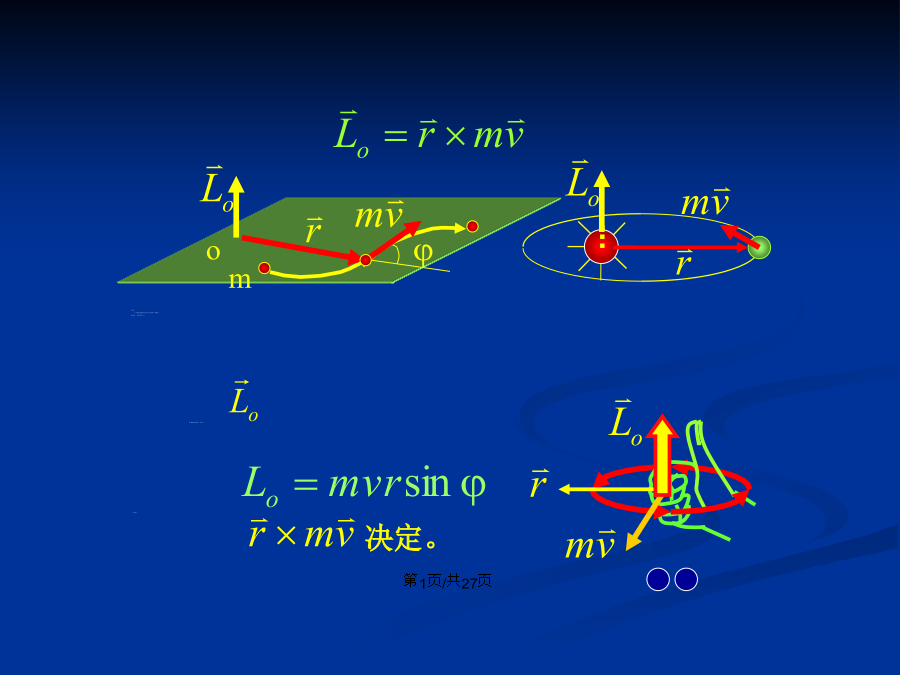
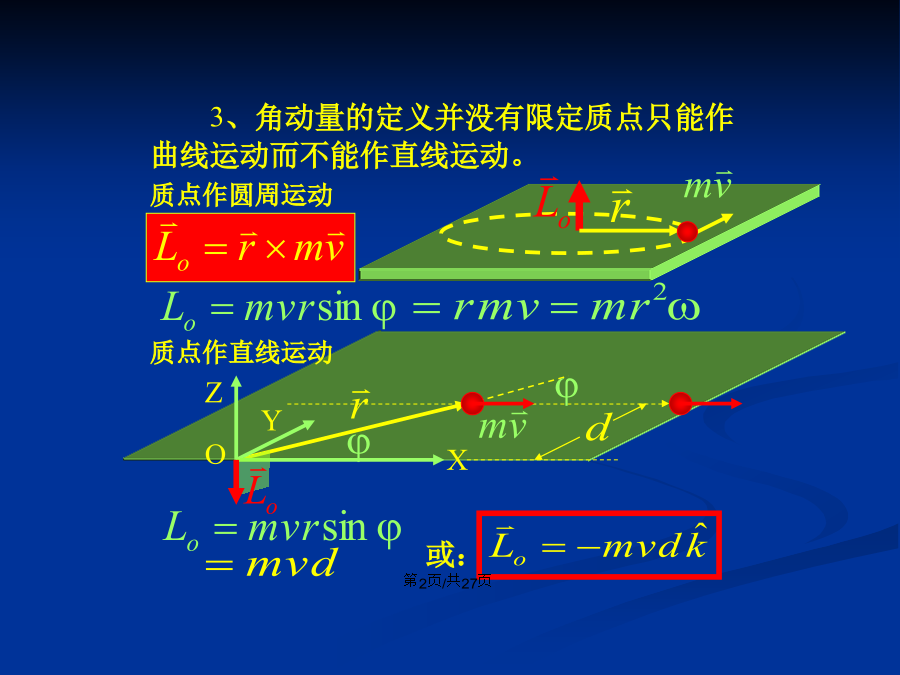
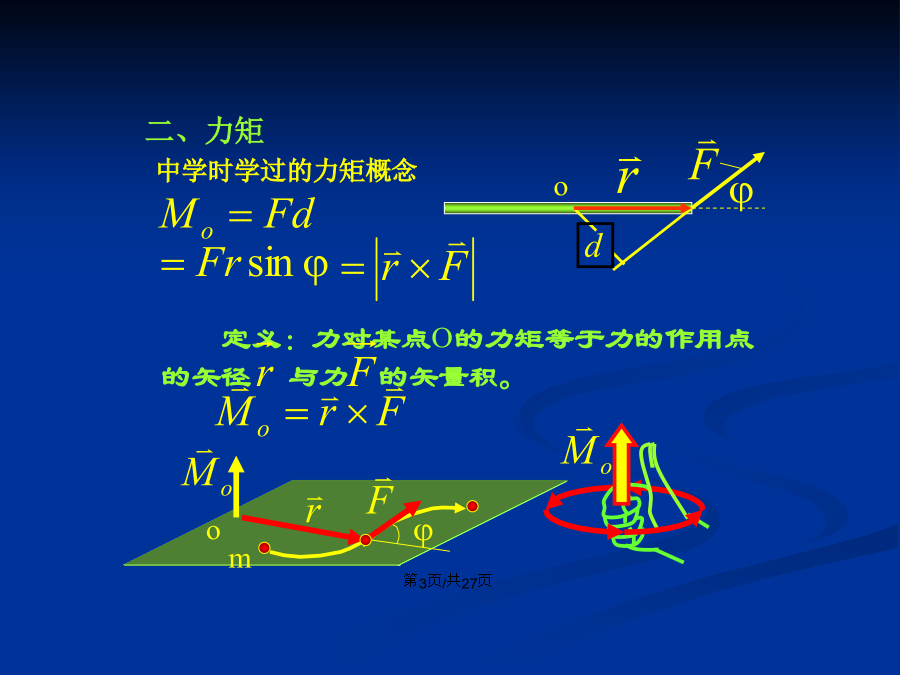
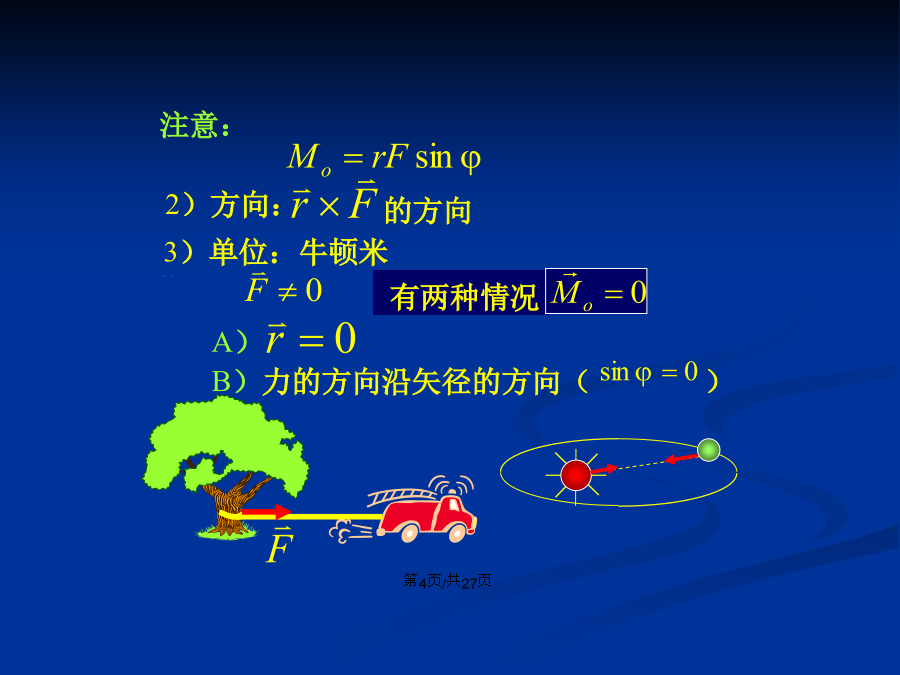
会计学3、角动量的定义并没有限定质点只能作曲线运动而不能作直线运动。注意：三、角动量定理令：2）角动量定理的积分形式四、角动量守恒定律例）用角动量守恒定律导出开普勒第二定律因为行星是在有心力的作用下运动的，对O点的外力矩为零，故角动量守恒，L为常量，又行星的质量是不变的，所以：例1：两个共轴飞轮转动惯量分别为J1、J2，角速度分别为1、2，求两飞轮啮合后共同的角速度。啮合过程机械能损失。共同角速度例2：彗星绕太阳作椭圆轨道运动，太阳位于椭圆轨道的一个焦点上，问系统的角动量是否守恒？近日点与远日点的速度谁大？由质点的角动量定义：近日点r小v大，远日点r大v，例2：光滑斜面倾角为，顶端固定一半径为R，质量为M的定滑轮，质量为m的物体用一轻绳缠在定滑轮上沿斜面下滑，求:下滑的加速度a。补充方程例3：质量为m、长为l的细杆一端固定在地面的轴上可自由转动，问当细杆摆至与水平面60º角和水平位置时的角加速度为多大。例4：质量为m、长为l的细杆两端用细线悬挂在天花板上，当其中一细线烧断的瞬间另一根细线中的张力为多大？以悬挂一端为轴，重力产生力矩。例5：在光滑水平桌面上放置一个静止的质量为M、长为2l、可绕中心转动的细杆，有一质量为m的小球以速度v0与杆的一端发生完全弹性碰撞，求小球的反弹速度v及杆的转动角速度。弹性碰撞机械能守恒，