
黏性流体的维定常流动.ppt

17****92








亲,该文档总共121页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

黏性流体的维定常流动.ppt
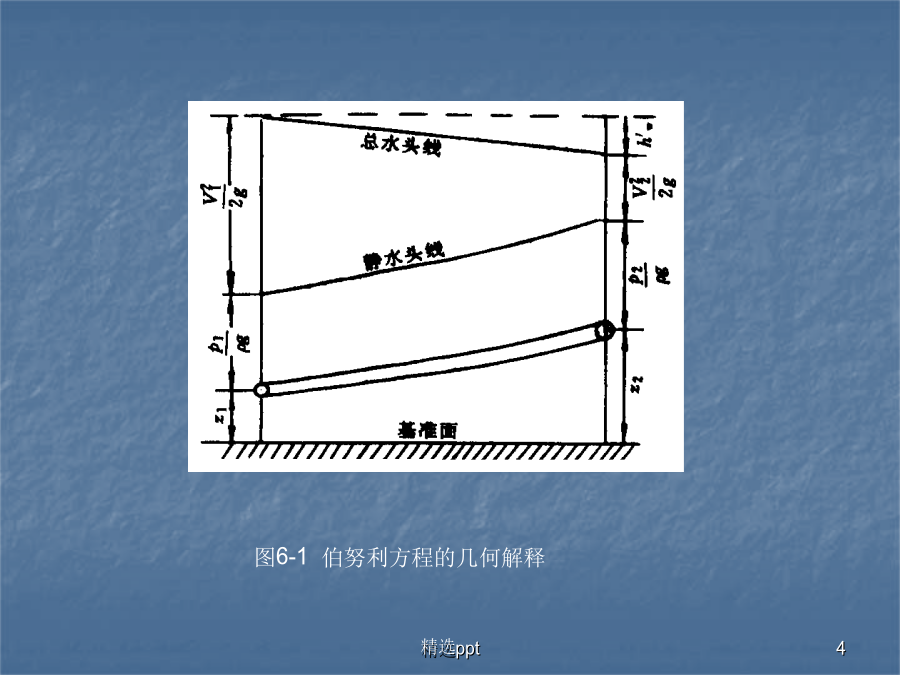
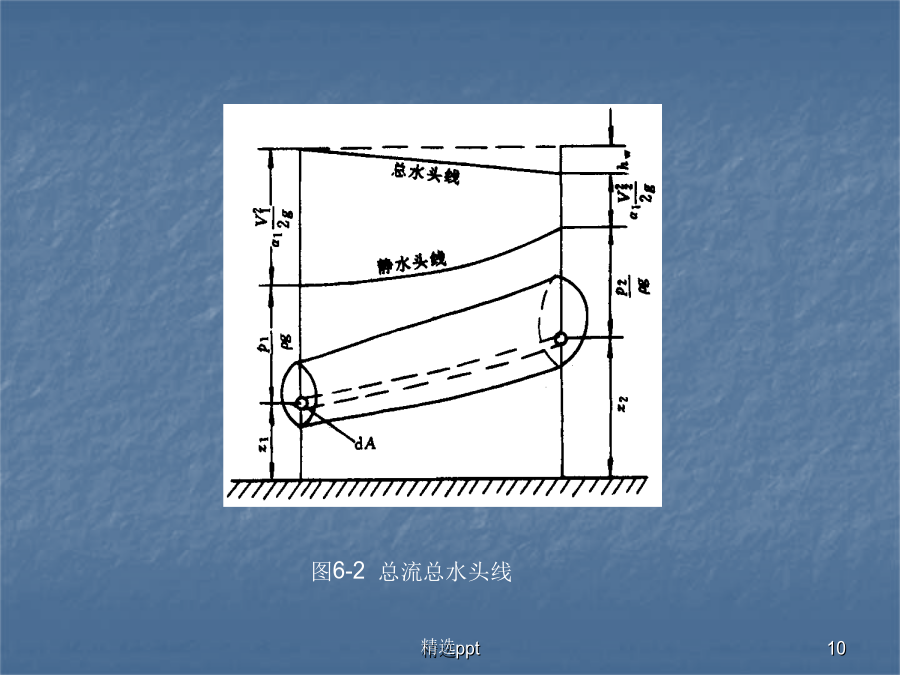
第六章粘性流体的一维定常流动在第三章中,通过对理想流体运动的基本规律的讨论,得到了流场中任一空间点上、任一时刻流体微团的压强和速度等流动参数之间的关系式,但在推导流体微团沿流线运动的伯努利方程中,仅局限于微元流束的范围内。而在工程实际问题中要研究实际流体在整个流场中的运动,其中大量的是在管道和渠道中的流动问题。所以除了必须把所讨论的范围从微元流束扩展到整个流场(如管道)外,还需考虑黏性对流体运动的影响,实际流体都具有黏性,在流动过程中要产生摩擦阻力,为了克服流动阻力以维持流动,流体中将有一部分机械能不可逆

第六章-黏性流体的一维定常流动.ppt
第六章粘性流体的一维定常流动在第三章中,通过对理想流体运动的基本规律的讨论,得到了流场中任一空间点上、任一时刻流体微团的压强和速度等流动参数之间的关系式,但在推导流体微团沿流线运动的伯努利方程中,仅局限于微元流束的范围内。而在工程实际问题中要研究实际流体在整个流场中的运动,其中大量的是在管道和渠道中的流动问题。所以除了必须把所讨论的范围从微元流束扩展到整个流场(如管道)外,还需考虑黏性对流体运动的影响,实际流体都具有黏性,在流动过程中要产生摩擦阻力,为了克服流动阻力以维持流动,流体中将有一部分机械能不可逆

第六章-黏性流体的一维定常流动.ppt
第六章粘性流体的一维定常流动在第三章中,通过对理想流体运动的基本规律的讨论,得到了流场中任一空间点上、任一时刻流体微团的压强和速度等流动参数之间的关系式,但在推导流体微团沿流线运动的伯努利方程中,仅局限于微元流束的范围内。而在工程实际问题中要研究实际流体在整个流场中的运动,其中大量的是在管道和渠道中的流动问题。所以除了必须把所讨论的范围从微元流束扩展到整个流场(如管道)外,还需考虑黏性对流体运动的影响,实际流体都具有黏性,在流动过程中要产生摩擦阻力,为了克服流动阻力以维持流动,流体中将有一部分机械能不可逆
黏性流体动量平衡方程纳维.ppt
[动量传入量][动量传出量]+[系统作用力的总和]=[动量蓄积量]⒉动量传递方式⒊作用力的形式⒋动量平衡方程的推导在直角坐标系中由于有三个方向的分速度,所以共有九个动量通量。以vx为准:动量通量2.3黏性流体动量平衡方程纳维-斯托克斯方程(Navier-Stokesequations)2.3黏性流体动量平衡方程纳维-斯托克斯方程(Navier-Stokesequations)2.3黏性流体动量平衡方程纳维-斯托克斯方程(Navier-Stokesequations)2.3黏性流体动量平衡方程纳维

流体力学第6章气体的一维定常流动ppt课件.ppt
第六章气体的一维定常流动第五章讨论的是不可压缩流体的流动,例如对于液体,即使在较高的压强下密度的变化也很微小,所以在一般情况下,可以把液体看成是不可压缩流体。对于气体来说,可压缩的程度比液体要大得多。但是当气体流动的速度远小于在该气体中声音传播的速度(即声速)时,密度的变化也很小。例如空气的速度等于50m/s,这数值比常温20℃下空气中的声速343m/s要小得多,这时空气密度的相对变化仅百分之一。所以为简化问题起见,通常也可忽略密度的变化,将密度近似地看作是常数,即在理论上把气体按不可压缩流体处理。当气体
